Introduction

Gibbs Sampling 是一種類似於 Metropolis Hasting 的抽樣方式，也是根據機率分佈來建立 Markov Chain ，並在 Markov Chain 上行走，抽樣出機率分佈。

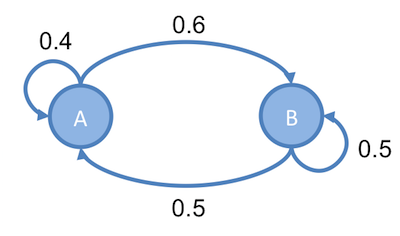
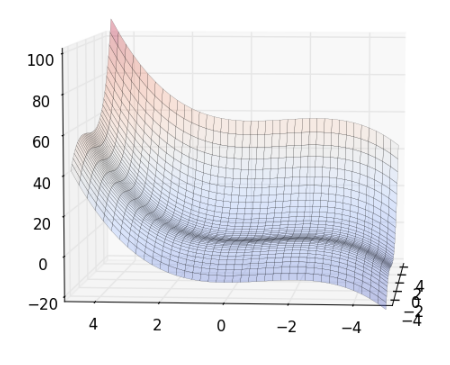
設一 Markov Chain ， 有 a 和 b 兩個 state ，它們的值分別為 $p(a)$ 和 $p(b)$ ，而它們之間的轉移機率，分別為 $q_1(a,b)$ 和 $q_2(a,b)$ ，如下圖：

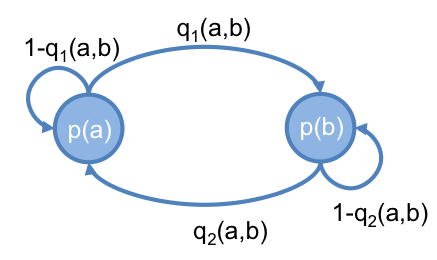
達平衡時，會滿足以下條件：

$$\begin{align} & \begin{bmatrix} p(a) \\ p(b) \end{bmatrix} = \begin{bmatrix} 1-q_1(a,b) & q_2(a,b) \\ q_1(a,b) & 1-q_2(a,b) \end{bmatrix} \begin{bmatrix} p(a) \\ p(b) \end{bmatrix} \\ & \Rightarrow \begin{cases} p(a)(1-q_1(a,b) +p(b)q_2(a,b) = p(a) \\ p(a)q_1(a,b) + p(b)(1-q_2(a,b)) = p(b) \end{cases}\\ & \Rightarrow p(a)q_1(a,b) = p(b)q_2(a,b) \end{align}$$

因此，達到平衡時，得出 （公式一） ：

$$p(a)q_1(a,b) = p(b)q_2(a,b)$$

在 Metropolis Hasting 這篇有提到，可以利用 Markov Chain 最終會達到平衡的特性，來為某機率分佈 $p(x)$ 抽樣。

但是 Metropolis Hasting 抽樣時，需要先用 proposed distribution 計算出下一個時間點可能的值，然後 acceptance probability 來拒絕它，因為計算出來的值會被拒絕，所以造成計算上的浪費。

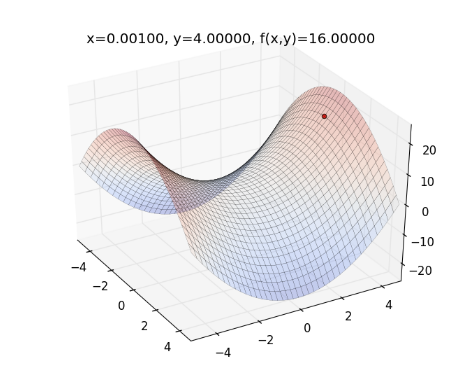
而對於一高維度的機率分佈 $p(x_1,x_2,...,x_n)$ ，可以用另一種方式來建立 Markov Chain ，則不會有這個問題。這種方法為 Gibbs Sampling 。

Introduction

對一個 Markov Chain 而言，不論起始狀態為多少，最後會達到一個穩定平衡的狀態。

舉個例子，以下為一 Markov Chain

則此 Markov Chain 達平衡狀態時， $A,B$ 的比率為$5:6$，也就是說：

$$\begin{align} & \begin{bmatrix} A \\ B \end{bmatrix} = \begin{bmatrix} 0.4 & 0.5 \\ 0.6 & 0.5 \end{bmatrix} \begin{bmatrix} A \\ B \end{bmatrix} \\ & \Rightarrow \begin{cases} 4A+5B = 10A \\ 6A+5B = 10B \end{cases}\\ & \Rightarrow 6A = 5B \end{align}$$

不管此 Markov Chain 的起始狀態如何，最後達平衡狀態時， $A,B$ 的比率一定為$5:6$。因此，如果在這 Markov Chain 的 $A$ 和 $B$ 任一一個點開始走，假設走的次數夠多的話，走到 $A$ 和走到 $B$ 的比例。會是 $5 : 6$ 。因此，可利用 Markov Chain 最後會收斂到一穩定狀態的特性，來進行抽樣。

Metropolis Sampler 即是給定一機率分佈函數，從這機率函數建立 Markov Chain ，然後再用建立出來的 Markov Chain 來進行抽樣。

Introduction

若某個有 $m$ 個維度的 data $\textbf{x} = \{x_1,x_2,...,x_m\}$ 的產生，是跟某個有 $n$個維度的 hidden variable $\textbf{z} = \{z_1,z_2,...,z_n\}$ 有關，在機率圖模型，表示成：

從這機率圖形，可得出 hidden variable $\textbf{z}$ 和 $\textbf{x}$ 的聯合分佈機率：

$$p(\textbf{x},\textbf{z}) = p(\textbf{z})p(\textbf{x}|\textbf{z})$$

若是給定 hidden variable $\textbf{z}$ 的值，則可產生 data $\textbf{x}$ ，如下：

$$p(\textbf{x}|\textbf{z})$$

但如果給定 data $\textbf{x}$ 的值，這組 data 所對應到的 hidden variable 的值，如下：

$$p(\textbf{z}|\textbf{x}) = \frac{p(\textbf{x} , \textbf{z})}{p(\textbf{x})} =\frac{p(\textbf{x} | \textbf{z}) p(\textbf{z}) }{\int p(\textbf{x} | \textbf{z})p(\textbf{z}) \text{d}\textbf{z}}$$

其中，分母 $\int p(\textbf{x} \mid \textbf{z})p(\textbf{z}) \text{d}\textbf{z}$ 積分如果無法算出來的時候，就無法直接算出 $p(\textbf{z}\mid \textbf{x})$ 的值，則要用估計的方法來計算 $p(\textbf{z}\mid \textbf{x})$ 的值。

Variational Inference 用來估計 $p(\textbf{z}\mid \textbf{x})$ 的值 。

AdaGrad

本文接續 Optimization Method – Gradient Descent & AdaGrad 。所提到的 AdaGrad ，及改良它的方法 – AdaDelta 。

在機器學習最佳化過程中，用 AdaGrad 可以隨著時間來縮小 Learning Rage ，以達到較好的收斂效果。AdaGrad 的公式如下：

$$\begin{align} & \textbf{G}_{t} = \sum_{n=0}^{t} \textbf{g}_{n}^{2} \\ & \textbf{x}_{t+1} = \textbf{x}_{t} - \frac{\eta}{\sqrt{\textbf{G}_{t}}} \textbf{g}_{t} \\ \end{align}$$

不過， AdaGrad 有個缺點，由於 $\textbf{g}_{n}^{2}$ 恆為正，故 $\textbf{G}_{t}$ 只會隨著時間增加而遞增，所以 $\frac{\eta}{\sqrt{\textbf{G}_{t}}}$ 只會隨著時間增加而一直遞減，如果 Learning Rate $\eta$的值太小，則 AdaGrad 會較慢才收斂。

舉個例子，如果目標函數為 $f(x,y) = y^2 - x^2$ ，起始點為 $(x,y) = (0.001,4)$ ， Learning Rate $\eta=0.5$ ，則整個最佳化的過程如下圖，曲面為目標函數，紅色的點為 $(x,y)$ ：

Gradient Descent

機器學習中，用 Gradient Descent 是解最佳化問題，最基本的方法。關於Gradient Descent的公式，請參考：Optimization Method – Gradient Descent & AdaGrad

對於 Cost function $f(\textbf{x})$ ，在 $\textbf{x} = \textbf{x}_{t}$ 時， Gradient Descent 走的方向為 $-\nabla f(\textbf{x})$ 。也就是，用泰勒展開式展開後，用一次微分 $f(\textbf{x})$ 來趨近的方向，如下圖：

註：考慮到 $\textbf{x}$ 為向量的情形，故一次微分寫成 $\nabla f(\textbf{x})$ 。

其中， $f(\textbf{x})$ 為原本的 Cost function ，而 $\tilde{f}(\textbf{x})$ 為泰勒展開式取一次微分逼近的。 而 Gradient Descent 走的方向為 $- \nabla f(\textbf{x})$ ，為沿著 $\tilde{f}(\textbf{x})$ 的方向。

Gradient Descent

在機器學習的過程中，常需要將 Cost Function 的值減小，通常用 Gradient Descent 來做最佳化的方法來達成。但是用 Gradient Descent 有其缺點，例如，很容易卡在 Local Minimum。

Gradient Descent 的公式如下：

$$\textbf{x}_{t+1} \leftarrow \textbf{x}_{t} - \eta \textbf{g}_{t}$$

關於Gradient Descent的公式解說，請參考：Optimization Method – Gradient Descent & AdaGrad

Getting Stuck in Local Minimum

舉個例子，如果 Cost Function 為 $0.3y^{3}+y^{2}+0.3x^{3}+x^{2}$ ，有 Local Minimum $(x=0,y=0)$ ，畫出來的圖形如下：

Introduction

在機器學習的過程中，常需要將 Cost Function 的值減小，需由最佳化的方法來達成。本文介紹 Gradient Descent 和 AdaGrad 兩種常用的最佳化方法。

Gradient Descent

Gradient Descent 的公式如下：

$$\textbf{x}_{t+1} \leftarrow \textbf{x}_{t} - \eta \textbf{g}_{t}$$

其中， $\eta$ 為 Learning Rate ， $\textbf{x}$ 為最佳化時要調整的參數， $\textbf{g}$ 為最佳化目標函數對 $\textbf{x}$ 的梯度。 $\textbf{x}_{t}$ 為調整之前的 $\textbf{x}$ ，$\textbf{x}_{t+1}$ 為調整之後的 $\textbf{x}$ 。

舉個例子，如果目標函數為 $f(x,y) = y^2 - x^2$ ，起始參數為 $(x,y) = (0.001,4)$ ，則畫出來的圖形如下圖，曲面為目標函數，紅色的點為起始參數：

Introduction

在解「 有條件的最佳化問題 」時，有時需要把原本的問題轉換成對偶問題(Dual Problem)後，會比較好解。

如果對偶問題有最佳解，原本問題也有最佳解，且這兩個最佳解相同，則必須要滿足 Karush-Kuhn-Tucker (KKT) Conditions：

1. Primal Feasibility

2. Dual Feasibility

3. Complementary Slackness

4. Stationarity

至於這四項到底是什麼？講起來有點複雜。本文會先從對偶問題的概念開始介紹，再來講解這四個條件。

The Lagrange dual function

首先，講解一下什麼是對偶問題。

通常，有條件的最佳化問題，可寫成 ＜公式一＞ ：

$$\begin{aligned} & \textbf{minimize} & f_{0}(x) & \\ & \textbf{subject to } & f_{i}(x) \leq 0 ,& i=1, ... ,m \\ & & h_{j}(x) = 0 , &j=1, ... ,p \\ \end{aligned}$$

Introduction

Recurrent Neural Network 在進行 Gradient Descent 的時候，會遇到所謂的 Vanishing Gradient Problem ，也就是說，在後面時間點的所算出的修正量，要回傳去修正較前面時間的參數值，此修正量會隨著時間傳遞而衰減。

為了改善此問題，可以用類神經網路模擬記憶體的構造，把前面神經元所算出的值，儲存起來。例如： Long Short-term Memory (LSTM) 即是模擬記憶體讀寫的構造，將某個時間點算出的值給儲存起來，等需要用它的時候再讀出來。

除了模擬單一記憶體的儲存與讀寫功能之外，也可以用類神經網路的構造來模擬 Turing Machine ，也就是說，有個 Controller ，可以更精確地控制，要將什麼值寫入哪一個記憶體區塊，或讀取哪一個記憶體區塊的值，這種類神經網路模型，稱為 Neural Turing Machine 。

如果可以模擬 Turing Machine ，即表示可以學會電腦能做的事。也就是說，這種機器學習模型可以學會電腦程式的邏輯控制與運算。

Neural Turing Machine

Neural Turing Machine 的架構如下：

Introduction

在數位電路裡面，如果一個電路沒有 latch 或 flip flop 這類的元件，它的輸出值只會取決於目前的輸入值，和上個時間點的輸入值是無關的，這種的電路叫作 combinational circuit 。

對於類神經網路而言，如果它的值只是從輸入端一層層地依序傳到輸出端，不會再把值從輸出端傳回輸入端，這種神經元就相當於 combinational circuit ，也就是說它的輸出值只取決於目前時刻的輸入值，這樣的類神經網路稱為 feedforward neural network 。

如果一個電路有 latch 或 flip flop 這類的元件，它的輸出值就跟上個時間點的輸入值有關，這種的電路它稱為 sequential circuit 。

所謂的 Recurrent Neural Network ，是一種把輸出端再接回輸入端的類神經網路，這樣可以把上個時間點的輸出值再傳回來，記錄在神經元中，達成和 latch 類似的效果，使得下個時間點的輸出值，跟上個時間點有關，也就是說，這樣的神經網路是有 記憶 的。

Recurrent Neural Network

由一個簡單神經元所構成的 Recurrent Neural Network ，構造如下：

這個神經元在 $t$ 時間，訓練資料的輸入值為 $x_{t}$ ，訓練資料的答案為 $y_{t}$ ，神經元 $n$ 的輸出值 $n_{out,t}$ ，可用以下公式表示：