Mark Chang's Blog

Machine Learning, Deep Learning and Python

AdaDelta

AdaGrad

本文接續 Optimization Method – Gradient Descent & AdaGrad 。所提到的 AdaGrad ，及改良它的方法 – AdaDelta 。

在機器學習最佳化過程中，用 AdaGrad 可以隨著時間來縮小 Learning Rage ，以達到較好的收斂效果。AdaGrad 的公式如下：

不過， AdaGrad 有個缺點，由於 恆為正，故 只會隨著時間增加而遞增，所以 只會隨著時間增加而一直遞減，如果 Learning Rate 的值太小，則 AdaGrad 會較慢才收斂。

舉個例子，如果目標函數為 ，起始點為 ， Learning Rate ，則整個最佳化的過程如下圖，曲面為目標函數，紅色的點為 ：

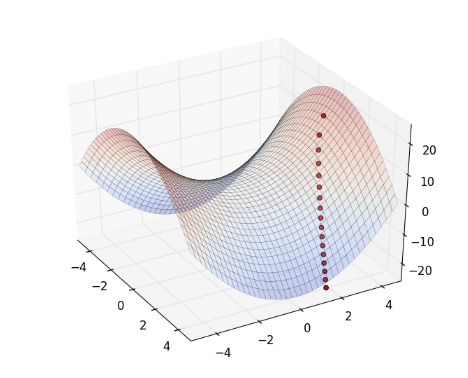
動畫版：

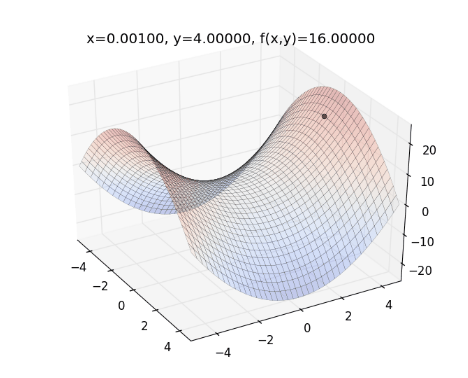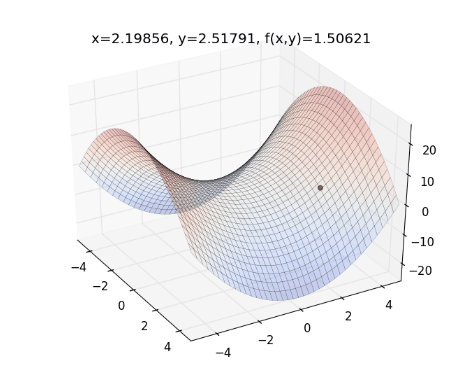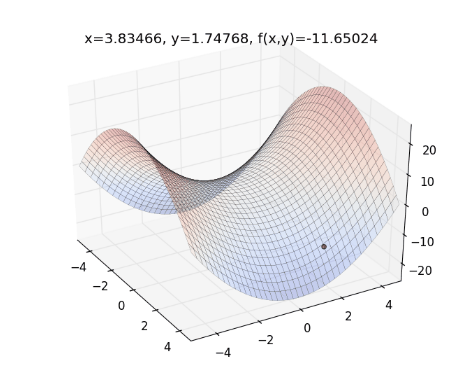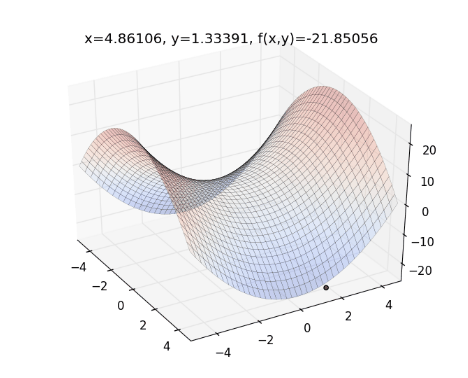
從上圖來看，一開始紅色點的下降速度很快，但越後面則越慢。

為了解決此問題，在調整 Learning Rate 時，不要往前一直加到最初的時間點，而只要往前加到某段時間即可。

但如果要從某段時間點的 開始累加，則需要儲存某個時間點之後開始的每個 ，這樣會造成記憶體的浪費。有種較簡便的做法，即是用衰減係數 ，將上一時間點的 乘上 ，如下：

藉由衰減係數 ，可讓較早期時間點累加的 衰減至 0 ，因此，不會使得 Learning Rate 只隨著時間而一直遞減。

Correct Units of ΔX

Adagrad 還有另一個問題，就是 的修正量– 為 ，假設它如果有「單位」的話，它的單位會與 不同。 因 的單位與 的單位相同，而會和 不同，因為：

註：在此假設 無單位。

相較之下， Newton’s Method 中， ， 的單位與 的單位相同，因為：

但 Newton’s Method 的缺點是，二次微分 Hessian 矩陣的反矩陣 ，計算時間複雜度太高。如果只是為了要單位相同，是沒必要這樣算。

想要簡易求出 的單位，稍微整理一下以上公式，得出：

因此，若要簡易求出 的單位，只要算 即可。

註：如果看不懂這段在寫什麼，請參考Matthew D. Zeiler. ADADELTA: AN ADAPTIVE LEARNING RATE METHOD.

AdaDelta

AdaDelta 解決了 AdaGrad 會發生的兩個問題：

(1) Learning Rate 只會隨著時間而一直遞減下去

(2) 與 的單位不同

AdaDelta 的公式如下：

其中， 和 為常數。 的作用為「衰減係數」，而 是為了避免 的分母為 0 。

此處的 有點類似 AdaGrad 裡面的 ，但如前面所述， AdaDelta 的不是直接把 直接累加上去，而是藉由衰減係數 ，可讓較早期時間點累加的 衰減至 0 ，因此，不會使得 Learning Rate 只隨著時間一直遞減下去。

而 的作用，則是使 與 有相同的單位，因為 與 具有相同單位，如下：

根據前一段的結果，若 ，則 與 的單位相同。

另外， 可累加過去時間點的 ，這樣所造成的效果，有點類似 Gradient Descent with Momentum ，使得現在時間點的 ，具有過去時間點的動量。

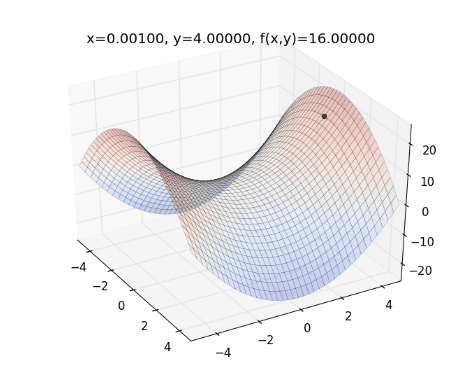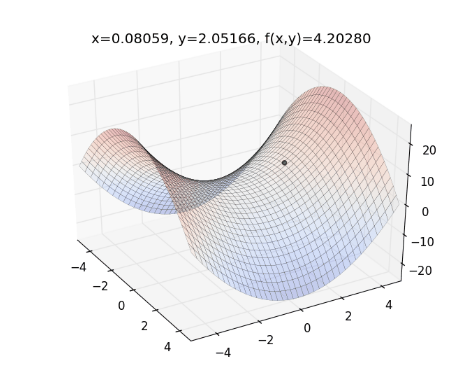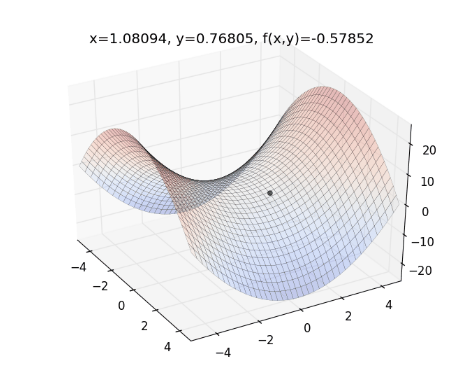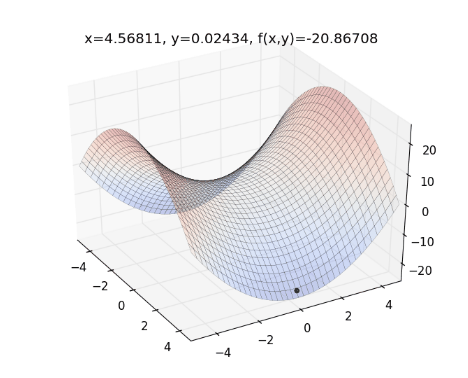
實際帶數字進去算一次 AdaDelta 。舉前述例子，假設 ，起始參數為 ，則畫出來的圖形如下圖，藍色點為起始點位置：

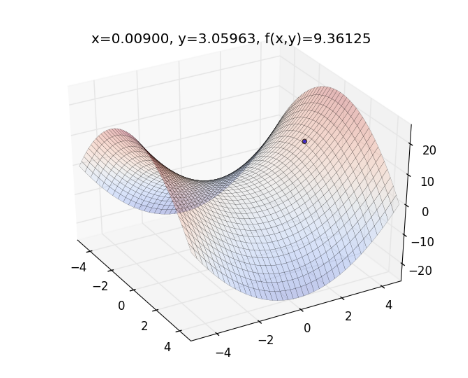
用 AdaDelta 最佳化方法，初始值設 ， ，設參數 ， ，更新 的值，如下，（註：以下的向量 、 、 等等的加減乘除運算，皆為 Element-wise Operation ）：

更新 的值， ，如下圖：

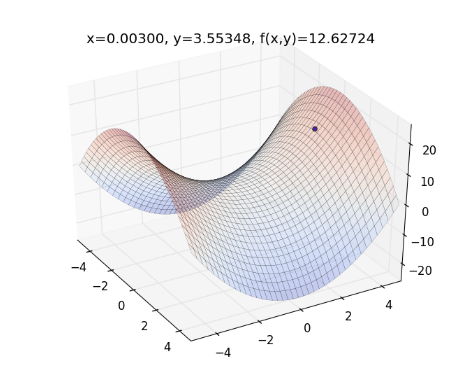
再往下走一步， 計算 的值，如下：

更新 的值， ，如下圖：

重複以上循環，整個過程如下圖：

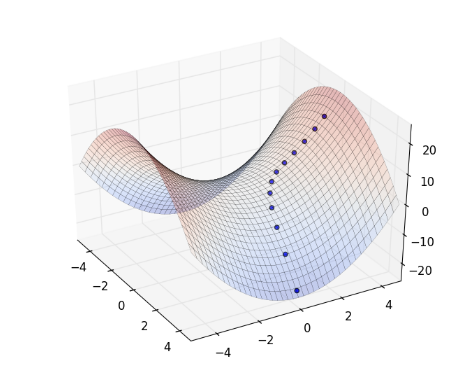
動畫版：

將 Gradient Descent （綠） ， AdaGrad （紅） 和 AdaDelta （藍） 畫在同一張圖上比較看看：

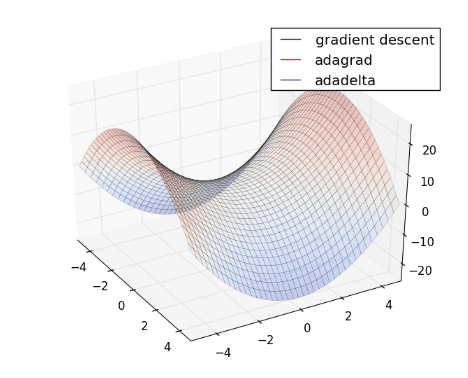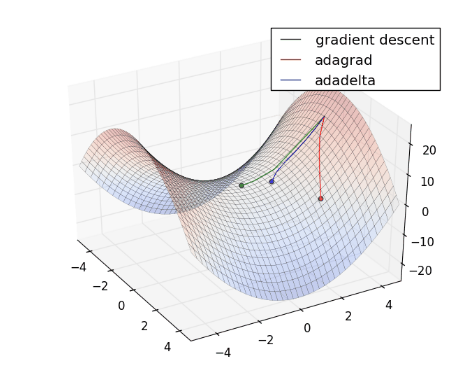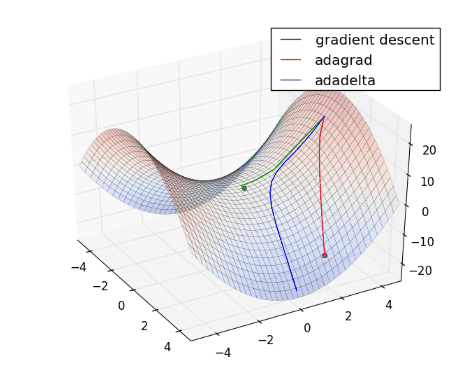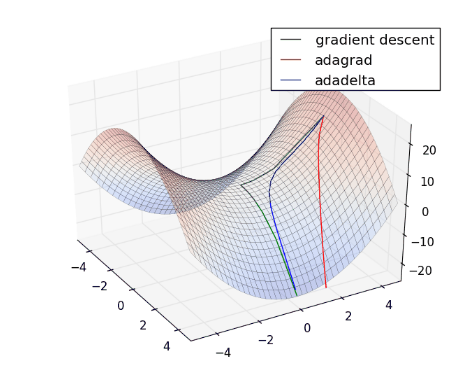
從上圖可看出， AdaDelta 的 Learning Rate 會隨著坡度而適度調整，不會一直遞減下去，也不會像 Gradient Descent 一樣，容易卡在 saddle point （請見 Optimization Method – Gradient Descent & AdaGrad ）。

Implementation

再來進入實作的部分

首先，開啟新的檔案 adadelta.py 並貼上以下程式碼：

adadelta.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np
from math import sqrt

XT = 0.001
YT = 4

def func(x,y):
  return (y**2-x**2)


def func_grad(x,y):
  return (-2*x, 2*y)


def plot_func(xt,yt,c='r'):
  fig = plt.figure()
  ax = fig.gca(projection='3d',
        elev=35., azim=-30)
  X, Y = np.meshgrid(np.arange(-5, 5, 0.25), np.arange(-5, 5, 0.25))
  Z = func(X,Y)
  surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1,
    cmap=cm.coolwarm, linewidth=0.1, alpha=0.3)
  ax.set_zlim(-50, 50)
  ax.scatter(xt, yt, func(xt,yt),c=c, marker='o' )
  ax.set_title("x=%.5f, y=%.5f, f(x,y)=%.5f"%(xt,yt,func(xt,yt)))
  plt.show()
  plt.close()


def run_adagrad():
  xt, yt = XT, YT
  eta = 0.5
  Gxt, Gyt = 0, 0
  plot_func(xt,yt,'r')
  for i in range(20):
    gxt, gyt = func_grad(xt, yt)
    Gxt += gxt**2
    Gyt += gyt**2
    xt -= eta*(1./(Gxt**0.5))*gxt
    yt -= eta*(1./(Gyt**0.5))*gyt
    if xt < -5 or yt < -5 or xt > 5 or yt > 5:
      break
    plot_func(xt,yt,'r')

def run_adadelta():
  xt, yt = XT, YT
  epsilon = 0.1
  rho = 0.5
  Gxt, Gyt = 0., 0.
  Dxt, Dyt = 0., 0.
  plot_func(xt,yt,'b')
  for i in range(20):
    gxt, gyt = func_grad(xt, yt)
    Gxt, Gyt = rho * Gxt + (1-rho) * (gxt**2) , rho * Gyt + (1-rho) * (gyt**2)
    dxt, dyt  = -(sqrt(Dxt + epsilon) / sqrt(Gxt + epsilon)) * gxt , \
                -(sqrt(Dyt + epsilon) / sqrt(Gyt + epsilon)) * gyt
    Dxt, Dyt =  rho * Dxt + (1-rho) * (dxt**2) , rho * Dyt + (1-rho) * (dyt**2)
    xt += dxt
    yt += dyt
    if xt < -5 or yt < -5 or xt > 5 or yt > 5:
      break
    plot_func(xt,yt,'b')

其中， func(x,y) 為目標函數， func_grad(x,y) 為目標函數的 gradient ，而 plot_func(xt,yt,c='r') 可畫出目標函數的曲面， run_adagrad() 用來執行 AdaGrad ， run_adadelta() 用來執行 AdaDelta 。

到 python console 執行：

1

>>> import adadelta

執行 AdaGrad ，指令如下：

1

>>> adadelta.run_adagrad()

則程式會逐一畫出整個過程：

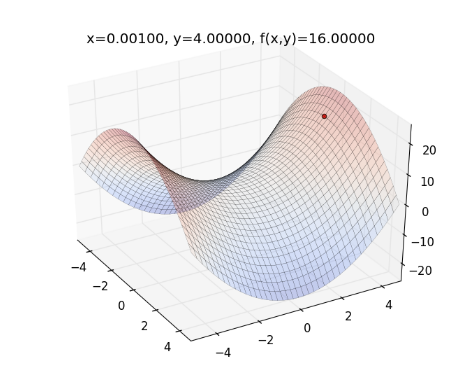
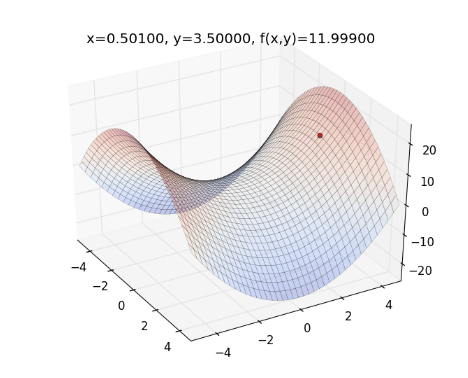
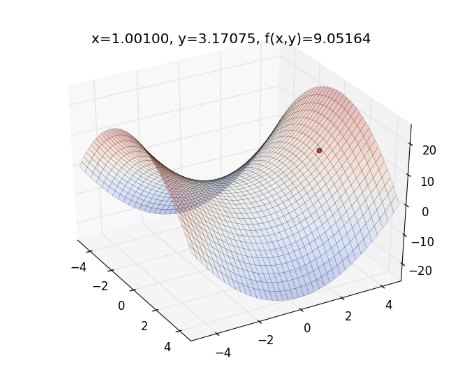
以此類推

執行 AdaDelta ，指令如下：

1

>>> adadelta.run_adadelta()

則程式會逐一畫出整個過程：

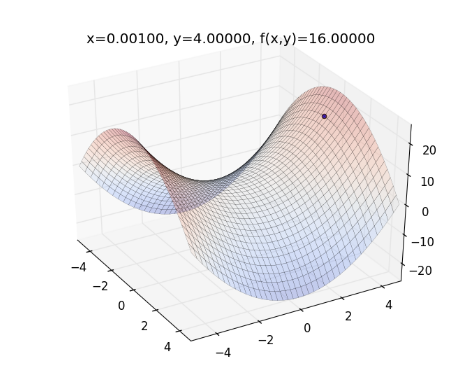
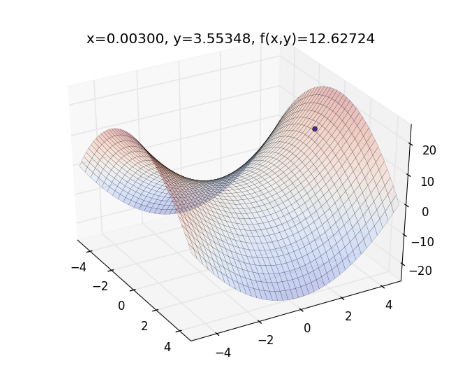
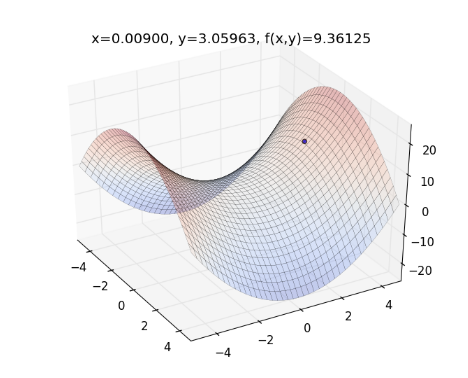
以此類推

Reference

Matthew D. Zeiler. ADADELTA: AN ADAPTIVE LEARNING RATE METHOD.

Visualizing Optimization Algos

Comments