Mark Chang's Blog

Machine Learning, Deep Learning and Python

Newton's Method for Optimization

Gradient Descent

機器學習中，用 Gradient Descent 是解最佳化問題，最基本的方法。關於Gradient Descent的公式，請參考：Optimization Method – Gradient Descent & AdaGrad

對於 Cost function ，在 時， Gradient Descent 走的方向為 。也就是，用泰勒展開式展開後，用一次微分 來趨近的方向，如下圖：

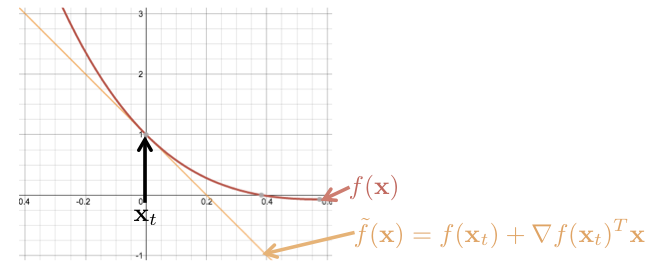
註：考慮到 為向量的情形，故一次微分寫成 。

其中， 為原本的 Cost function ，而 為泰勒展開式取一次微分逼近的。 而 Gradient Descent 走的方向為 ，為沿著 的方向。

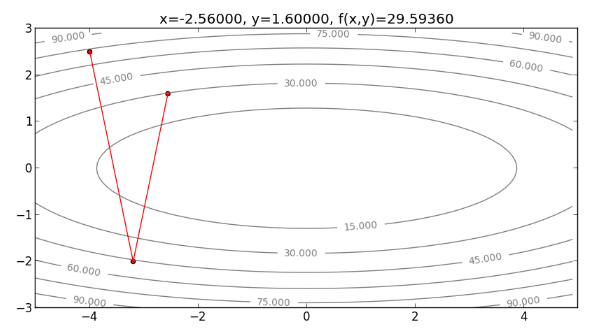
這會有個問題，如果原本的 Cost function 為較高次函數，只用一次項來逼近是不夠的，有時候，失真情形很嚴重，例如， Cost function 為橢圓 ， 此函數的等高線圖，如下圖：

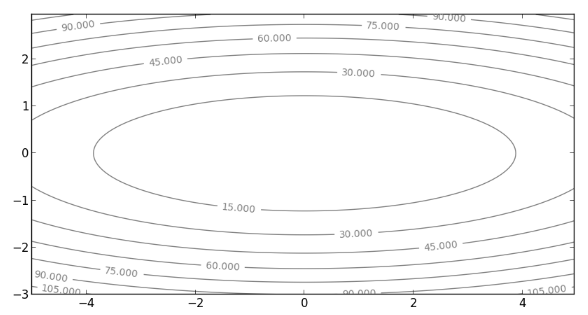
如果起始點為 ，沿著 的方向走，也就是說，走梯度最陡的方向（即與等高線垂直的方向），可能會需要多次折返，才能走到最小值，如下圖：

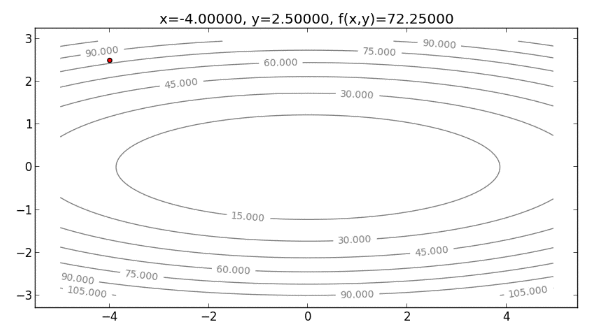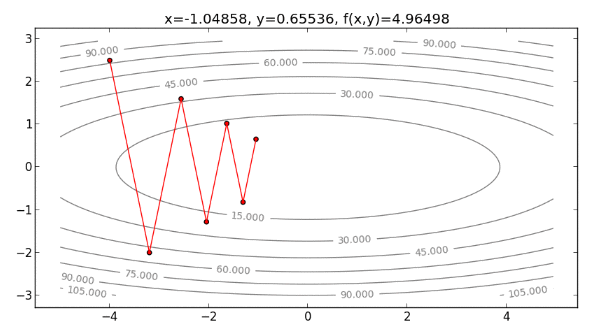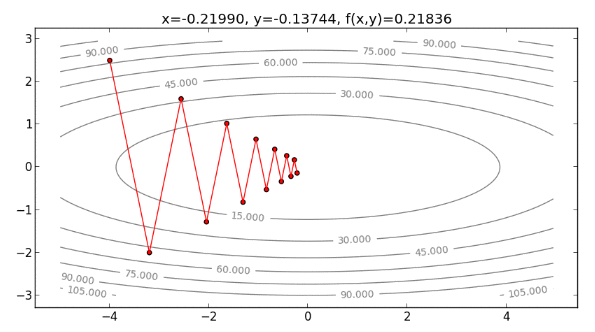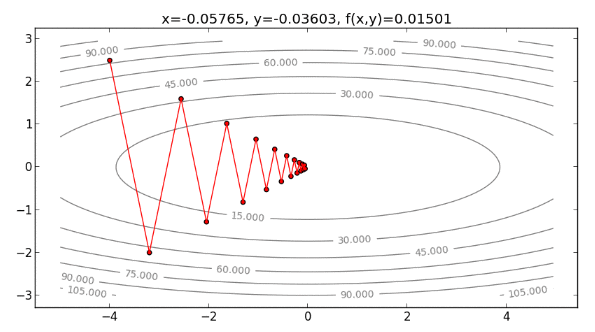
Second-Order Taylor Approximation

根據前面的例子得知，只考慮一次微分項，是不夠的，現在要來考慮二次微分項。

對於 Cost function ， 在 時，用泰勒展開式展開後，分別用一次微分與二次微分來逼近，如下圖：

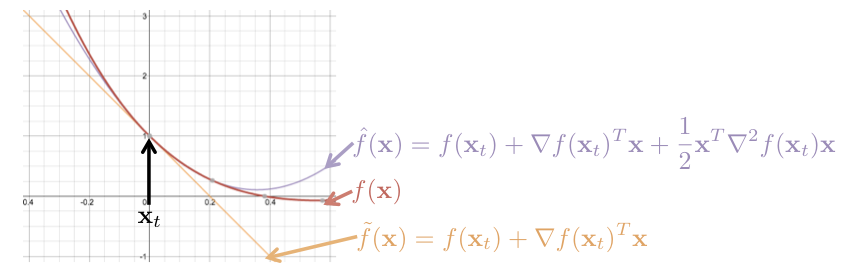
其中，橘色的 為只用了一次微分的逼近，而紫色的 為用了一次與二次微分向的逼近，由此可見， 較 接近原本的

如果要求 的最小值，可以往 為最小值的方向，一步一步走下去。要找出 的最小值，即：

將 對 微分，令微分結果為 ，得：

得

可以用此 ，來當作位於 時，想走往 的最小值，要走的方向（與距離）。用一次與二次微分所得出的方向，一步步走下去，最後走到最小值，這種方法即為 Newton’s Method 。

Newton’s Method for Optimization

Newton’s Method 即是考慮二次微分的 Gradient Descent 方法，公式如下：

其中， 為 Learning Rate ， （ 稱為 Hessian ）， （ 稱為 Gradient ）。

再來看看用 Newton’s Method 來解決 Cost function 為橢圓 的情形。首先，畫出起始點 ，如下圖：

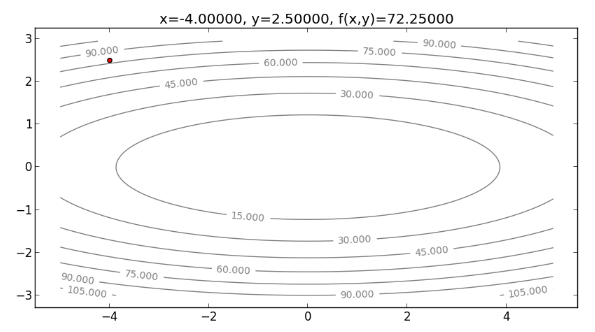
先來算 和 ，分別為：

設 ，代入起始點 、 和 到 Newton’s Method 的公式： ，得：

更新圖上的點， ，如下圖：

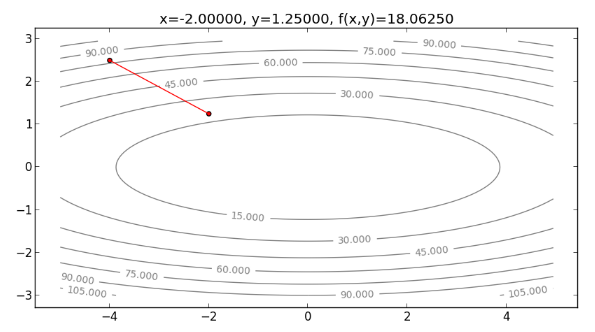
再往下走一步，求 的值，如下：

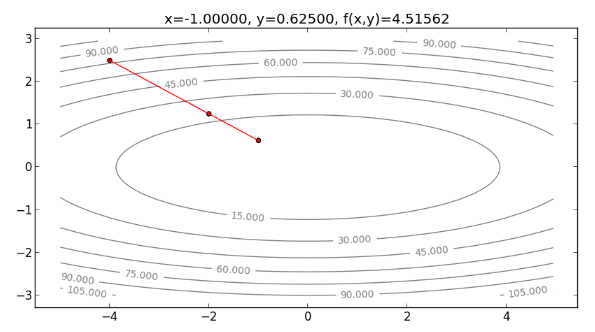
從以上過程發現， Newton’s Method 方向不需要一直折返，可以直接往最小值處走下去 ，整個過程如下圖：

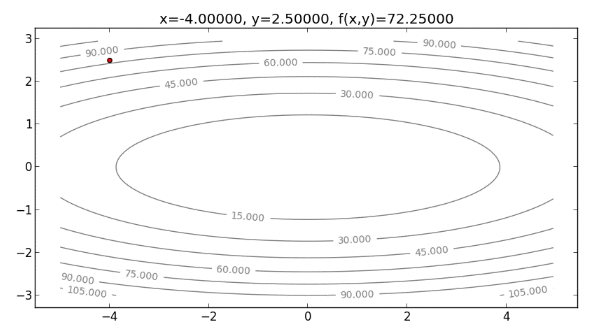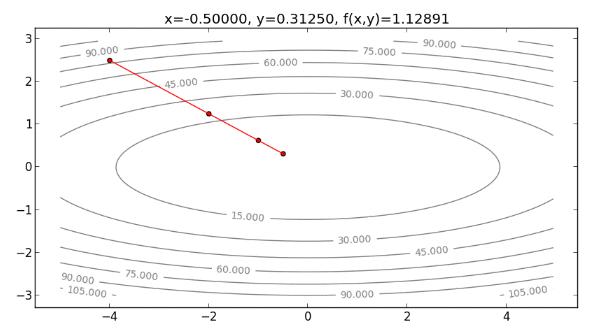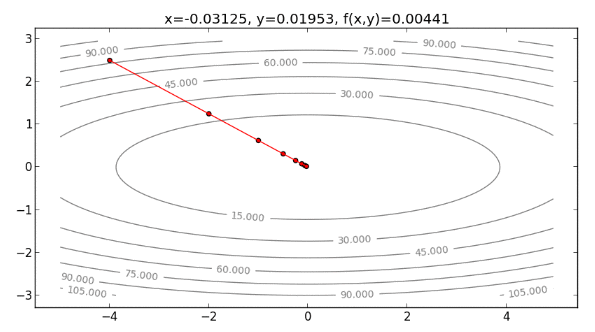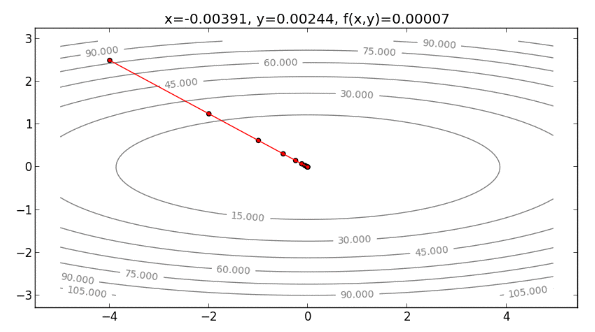
註：事實上，由於本例的 Cost function 為二次函數，如果是用二次的泰勒展開式逼近，則可以完全貼合 。所以用 Newton’s Method 的話， 位於 時， 即是泰勒展開式最小值的 解，也是 的最小值解，如果設 ，只要走一步就可以走到最小值，如下：

過程如下圖所示：

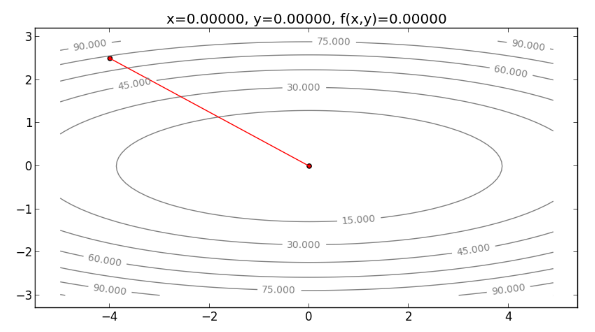
Implementation

再來進入實作的部分

首先，開啟新的檔案 newtons.py 並貼上以下程式碼：

newtons.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

import numpy as np
import matplotlib.pyplot as plt

A = 1
B = 9


def obj_func(x, y):
    z = A*(x**2) + B*(y**2)
    return z


def obj_func_grad(x, y):
    return np.array([2*A*x, 2*B*y])


def obj_func_hessian(x, y):
    return np.array([[2*A, 0],
                     [0, 2*B]
                     ])


def plot_func(xts, yts, c):
    delta = 0.1
    x = np.arange(-5.0, 5.0, delta)
    y = np.arange(-3.0, 3.0, delta)
    X, Y = np.meshgrid(x, y)
    Z = obj_func(X, Y)
    plt.figure(figsize=(10, 5))
    CS = plt.contour(X, Y, Z, colors='gray')
    plt.plot(xts, yts, c='r')
    for xt, yt in zip(xts, yts):
            plt.scatter(xt, yt, c='r')
    plt.title("x=%.5f, y=%.5f, f(x, y)=%.5f"%(xts[-1], yts[-1], obj_func(xts[-1], yts[-1])))
    plt.clabel(CS, inline=1, fontsize=10)
    plt.show()


def run_gd():
    xy = np.array([-4, 2.5])
    eta = 0.1
    xts = [xy[0]]
    yts = [xy[1]]
    plot_func(xts, yts, 'r')
    for i in range(1, 20):
        gxy = obj_func_grad(xy[0], xy[1])
        xy -= eta * gxy
        xts.append(xy[0])
        yts.append(xy[1])
        plot_func(xts, yts, 'r')


def run_newtons():
    xy = np.array([-4, 2.5])
    eta = 0.5
    xts = [xy[0]]
    yts = [xy[1]]
    plot_func(xts, yts, 'b')
    for i in range(1, 20):
        gxy = obj_func_grad(xy[0], xy[1])
        hxy = obj_func_hessian(xy[0], xy[1])
        deltax = np.dot(np.linalg.inv(hxy), gxy)
        xy -= eta * deltax
        xts.append(xy[0])
        yts.append(xy[1])
        plot_func(xts, yts, 'b')

其中， obj_func(x,y) 為目標函數， obj_func_grad(x,y) 為 ， obj_func_hessian(x,y) ，而 plot_function(xt,yt,c='r') 可畫出目標函數的等高線圖， run_gd() 用來執行 Gradient Descent ， run_newtons() 用來執行 Newton’s Method 。 xy 對應到前例的 ，而 eta 為 Learning Rate 。 for i in range(20) 表示最多會跑20個迴圈。

到 python console 執行：

newtons.py
1

>>> import newtons

執行 Gradient Descent ，指令如下：

newtons.py
1

>>> newtons.run_gd()

則程式會逐一畫出整個過程：

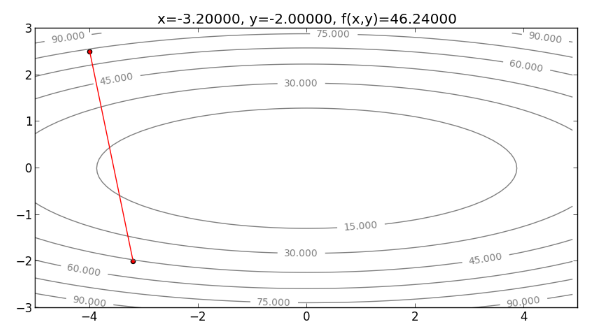
以此類推

執行 Newton’s Method ，指令如下：

newtons.py
1

>>> netons.run_newtons()

則程式會逐一畫出整個過程：

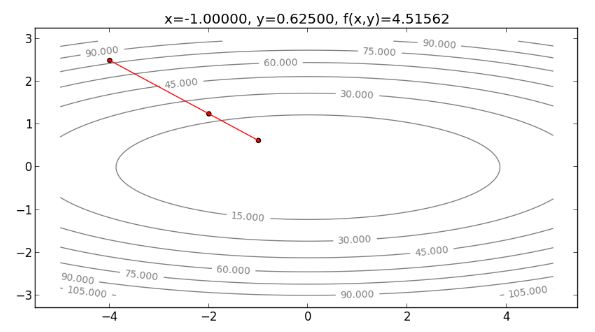
以此類推

Comment

Newton’s Method 需要計算二次微分 Hessian 矩陣的反矩陣，如果 variable 為高維度向量，則計算這個矩陣的時間複雜度會很高，而且很占記憶體空間，因此有人提出一些 Hessian 矩陣的近似求法，例如 L-BFGS 。但如果用在像是 Deep Learning 這種有超多 variable 的模型，近似求法仍然太慢，因此解 Deep Learning 問題，通常只會用一次微分的方法，例如 Adagrad之類的。

Reference

本文參考至以下教科書：

Stephen Boyd & Lieven Vandenberghe. Convex Optimization. Chapter 5 Duality.

Comments