Metropolis Hasting

Introduction

對一個 Markov Chain 而言，不論起始狀態為多少，最後會達到一個穩定平衡的狀態。

舉個例子，以下為一 Markov Chain

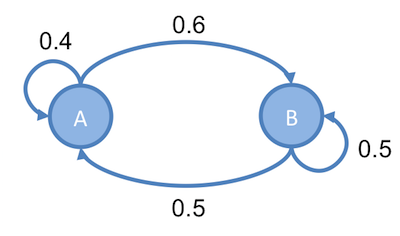
則此 Markov Chain 達平衡狀態時， $A,B$ 的比率為 $5:6$ ，也就是說：

$\begin{align} & \begin{bmatrix} A \\ B \end{bmatrix} = \begin{bmatrix} 0.4 & 0.5 \\ 0.6 & 0.5 \end{bmatrix} \begin{bmatrix} A \\ B \end{bmatrix} \\ & \Rightarrow \begin{cases} 4A+5B = 10A \\ 6A+5B = 10B \end{cases}\\ & \Rightarrow 6A = 5B \end{align}$

不管此 Markov Chain 的起始狀態如何，最後達平衡狀態時， $A,B$ 的比率一定為 $5:6$ 。因此，如果在這 Markov Chain 的 $A$ 和 $B$ 任一一個點開始走，假設走的次數夠多的話，走到 $A$ 和走到 $B$ 的比例。會是 $5 : 6$ 。因此，可利用 Markov Chain 最後會收斂到一穩定狀態的特性，來進行抽樣。

Metropolis Sampler 即是給定一機率分佈函數，從這機率函數建立 Markov Chain ，然後再用建立出來的 Markov Chain 來進行抽樣。

Metropolis Sampler

設某一機率分佈 $p(X)$ ，起始值為 $x_{0}$ 。隨機變數的值為 $X = \{ a_{1}, a_{2}, ..., a_{n}\}$ 。

抽樣過程如下：

設目前時間點 $t$ 抽出的值為 $x_{t}=a_{i}$ 然後，從一機率分佈（稱為 proposal distribution）， $q(x_{t+1}\mid x_{t})$ 中，抽出一個值，為 $a_{j}$ ，其中 $q(x_{t+1}\mid x_{t})$ 滿足以下對稱性即可：

$q(x_{t+1}|x_{t}) = q(x_{t}|x_{t+1})$

$q(x_{t+1}\mid x_{t})$ 可以是比較好計算的函數，用於快速產生下一個可能的樣本 $a_{j}$ ， $a_{j}$ 為 proposed state ，意思就是說，想從 $q(x_{t+1}\mid x_{t})$ 「提出」一個值，看看這個值能不能成為 $x_{t+1}$ 的值，但實際上，這時還不知道 $a_{j}$ 適不適合為 $x_{t+1}$ 的值，所以要做以下運算。

如果 $p(a_{j}) \geq p(a_{i})$ ，則：

$x_{t+1} = a_{j}$

如果 $p(a_{j}) < p(a_{i})$ 則：

$\begin{align} & x_{t+1} = \begin{cases} a_{j} & \text{with probability of } \alpha \\ a_{i} & \text{with probability of } 1- \alpha \end{cases}\\ & \text{where } \alpha = \frac{p(a_j)}{p(a_{i})} \end{align}$

其中， $\alpha$ 稱為 acceptance probability ，意思是，接受 $x_{t+1}$ 的值為 $a_{j}$ 的機率有多少？

此方法可以看成是在 $a_{i}$ 與 $a_{j}$ 之間，建立 Markov Chain ：

如果想從 $a_{i}$ 轉移到 $a_{j}$ ，且， $p(a_{j}) \geq p(a_{i})$ ，則建立出的 Markov Chain ，如下：

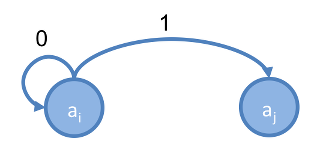
由於 $p(a_{j}) \geq p(a_{i})$ ，所以一定會接受從 $a_{i}$ 到 $a_{j}$ 的轉移。

呈上，如果想從 $a_{j}$ 轉移回 $a_{i}$ ，則建立出的 Markov Chain ，如下：

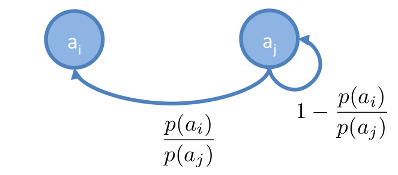
由於 $p(a_{i}) < p(a_{j})$ ，所以從 $a_{j}$ 轉到 $a_{i}$ 的轉移，不一定會成立，而是由 acceptance probability 來決定。

把以上兩個合起來，得出 $a_{i}$ 與 $a_{j}$ 之間的 Markov Chain ，如下：

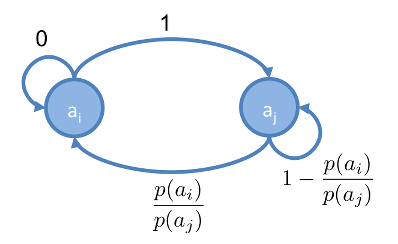
假設在這 Markov Chain 上，隨機走動，設走到 $a_i$ 的機率為 $A$ ，走到 $a_j$ 的機率為 $B$ ，則達平衡時：

$\begin{align} & \begin{bmatrix} A \\ B \end{bmatrix} = \begin{bmatrix} 0 & \frac{p(a_i)}{p(a_j)} \\ 1 & 1 - \frac{p(a_i)}{p(a_j)} \end{bmatrix} \begin{bmatrix} A \\ B \end{bmatrix} \\ & \Rightarrow \begin{cases} \frac{p(a_i)}{p(a_j)} B = A \\ A + (1 - \frac{p(a_i)}{p(a_j)})B = B \end{cases}\\ & \Rightarrow A : B = p(a_i) : p(a_j) \end{align}$

因此 Markov Chain 達到平衡狀態時，走到 $a_i$ 和走到 $a_j$ 的次數比，會是 $p(a_i):p(a_j)$ 。

舉個簡單的例子，假設 $p(x)$ 如下， $X$ 有0.8的機率為 0 ，有0.2的機率為 1 ，如下：

$p(x) = \begin{cases} 0.2 & X=0 \\ 0.8 & X=1 \end{cases}\\$

則建立出來的 Markov Chain 如下圖：

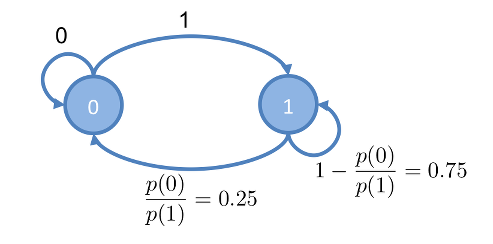
從這 Markov Chain 上，從 0 開始走，會先轉移到 1 ，走過的序列如下：

01

到 1 以後，有 0.75的機率會走回 1，有0.25會再走到 0 ，走到 1 和走到 0 的比率是 3:1 ，假設走回 1 三次以後才走回0 ，則走過的序列如下：

011110

這樣一直走下去，則

01111011110111101111...

序列中任取一個數，則有0.8的機率為 0 ，有0.2的機率為 1 ，和 $p(x)$ 的機率分佈一樣。

因此，建立了 $a_{i}$ 與 $a_{j}$ 之間的 Markov Chain 之後，就可以在這兩個點上面來回行走，抽出適當比例的樣本。

可以把 $X$ 只有兩個值的機率分佈，推廣到多個值，在 $X = \{ a_{1}, a_{2}, ..., a_{n}\}$ 中的任兩個值都可以建立這樣的 Markov Chain ，在這些 Markov Chain 中，來回行走，最後達平衡時，抽出來的序列就等同於從 $p(X)$ 的機率分佈中抽樣。

整個抽樣過程的 pseudo code 如下：

$\begin{align} 1 & \text{set }t = 0 \\ 2 & \text{generate an initial state } x_0 \in \{ a_{1}, a_{2}, ..., a_{n}\} \\ 3 & \text{repeat until }t = M \\ 4 & \mspace{30mu} \text{generate a proposal state } a_{j} \text{ from } q(x_{t+1} | x_t ) \\ 5 & \mspace{30mu} \text{calculate the acceptance probability }\alpha = \text{min} \left(1,\frac{p(a_{j})}{p(x_t)} \right) \\ 6 & \mspace{30mu} \text{draw a random number } u \text{ from } \text{Unif}(0,1) \\ 7 & \mspace{30mu} \text{if }u \leq \alpha \\ 8 & \mspace{60mu} \text{ accept the proposal state } a_{j} \text{ and set } x_{t+1}= a_{j} \\ 9 & \mspace{30mu} \text{else set } \\ 10 & \mspace{60mu} x_{t+1} = x_{t} \end{align}$

其中， $M$ 為抽出的樣本數，而從 Unif(0,1) 抽出的 $u$ ，目的是要讓 $x_{t+1}= a_{j}$ 成立的機率為 $\alpha$ 。

由於 Metropolis Sampler 的 proposed distribution 一定要滿足對稱性，如果 $p(x)$ 為非對稱性的機率分佈，例如 Gamma distribution ，就不太適合用對稱性的 proposed distribution 來進行抽樣。

Metropolis Hasting 是一種更 General 的抽樣方式，它可用於以下情形：

$q(x_{t+1}|x_{t}) \neq q(x_{t}|x_{t+1})$

如果 $q(x_{t+1}\mid x_{t})$ 不對稱，例如 $q(x_{t+1}\mid x_{t}) > q(x_{t}\mid x_{t+1})$ 這種情況，表示從 $x_{t}$ 的位置「提出」走到 $x_{t+1}$ 的位置，機率是比從 $x_{t+1}$ 「提出」走回 $x_{t}$ 還高。所以也要把這個機率的差異考慮到 Markov Chain 裡面，因此要加入 correction factor $c$ ：

$c = \frac{q(x_{t}|x_{t+1})}{q(x_{t+1}|x_{t})}$

將 $c$ 乘上 proposed probability ，來修改 acceptance probability ：

$\alpha = \frac{p(a_j)}{p(a_{i})} \times c = \frac{p(a_j)}{p(a_{i})} \times \frac{q(a_i|a_j)}{q(a_j|a_i)}$

如果要在 $a_i$ 與 $a_j$ 之間，建立 Markov Chain ，且 $p(a_j)q(a_i\mid a_j) > p(a_{i})q(a_j\mid a_i)$ ，則建立出的 Markov Chain ，如下：

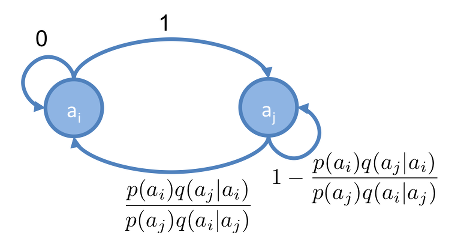
除了 acceptance probability 要加上 correction factor 之外， Metropolis Hasting 的抽樣過程，幾乎和 Metropolis Sampler 一樣。整個抽樣過程的 pseudo code 如下：

$\begin{align} 1 & \text{set }t = 0 \\ 2 & \text{generate an initial state } x_0 \in \{ a_{1}, a_{2}, ..., a_{n}\} \\ 3 & \text{repeat until }t = M \\ 4 & \mspace{30mu} \text{generate a proposal state } a_{j} \text{ from } q(x_{t+1} | x_t ) \\ 5 & \mspace{30mu} \text{calculate the proposal correction factor }c = \frac{q(x_{t-1} | a_j) }{q(a_j|x_{t-1})} \\ 6 & \mspace{30mu} \text{calculate the acceptance probability }\alpha = \text{min} \left(1,\frac{p(a_{j})}{p(x_t)} \times c \right) \\ 7 & \mspace{30mu} \text{draw a random number } u \text{ from } \text{Unif}(0,1) \\ 8 & \mspace{30mu} \text{if }u \leq \alpha \\ 9 & \mspace{60mu} \text{ accept the proposal state } a_{j} \text{ and set } x_{t+1}= a_{j} \\ 10 & \mspace{30mu} \text{else set } \\ 11 & \mspace{60mu} x_{t+1} = x_{t} \end{align}$

Implementation

再來，進入實作的部分

Metropolis Sampler

首先，從 Metropolis Sampler 開始，用 Metropolis Sampler 對以下 $p(x)$ 進行抽樣：

$p(x) = \begin{cases} 0.2 & X=0 \\ 0.8 & X=1 \end{cases}\\$

程式碼如下：

matrosamp.py

import random
import collections


def metrosamp(ITER):
    P = {0: 0.2, 1: 0.8}
    Q = {1: 0, 0: 1}
    X = []
    xt = 0
    for i in range(ITER):
        xtp1 = Q[xt]
        alpha = min(1., P[xtp1] / P[xt])
        if random.random() <= alpha:
            xt = xtp1
        X.append(xt)
    return X


def count(X):
    counter = collections.Counter(X)
    for key in counter:
        print key, counter[key]

程式碼中的 P 即 $p(x)$ ，而 Q 則是 proposed distribution ， $q(x_{t}\mid x_{t-1})$ ：

$\begin{align} & q(x_{t} = 0 |x_{t-1}=1) = 1 \\ & q(x_{t} = 1|x_{t-1}=0) = 1 \\ \end{align}$

也就是說，位於 0 時， proposed distribution 會「提出」走到 1 ，位於 1 時會提出走到 0 。

而進行 Metropolis Sampler 抽樣的演算法為程式碼中的 metrosamp ，抽樣結果儲存於 X ：

>>> X = metrosamp(10000)
>>> print X
[1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1,....]

用count` 則是將結果做統計：

>>> count(X)
0 2027
1 7973

0 和 1 的比例，接近 0.2 和 0.8 。

Metropolis Hasting

再來舉個 Metropolis Hasting 的例子。

Metropolis Hasting 也可以用在連續的機率分佈，此例用 Metropolis Hasting 來對 gamma distribution 進行抽樣，程式碼如下：

metrohast.py

import numpy as np
import random
import collections
import matplotlib.pyplot as plt
import math
import scipy.stats

def p_func_raw(x, a, b):
    S1 = ((b ** a) / math.gamma(a))
    S2 = x ** (a - 1)
    S3 = math.exp(-b * x)
    return S1 * S2 * S3  # * S4

def p_func(y):
    return p_func_raw(y, 2, 1)

def q_func(beta):
    return np.random.exponential(beta)

def q_func_pdf(x, beta):
    return scipy.stats.expon.pdf(x, scale=beta)

def metrohast(M):
    X = []
    beta = 5.
    xt = beta
    for i in range(M):
        aj = q_func(beta)
        c = q_func_pdf(xt, beta) / q_func_pdf(aj, beta)
        alpha = min(1., (p_func(aj) / p_func(xt)) * c)
        if random.random() <= alpha:
            xt = aj
        X.append(xt)
    return X

def draw(S):
    n, bins, patches = plt.hist(S, 100, normed=1, facecolor='b', alpha=0.2)
    plt.plot(bins, [p_func(x) for x in bins], color='r')
    plt.show()

本例實作一個 gamma distribution 的抽樣：

$Gamma(x,a,b) = \frac{ b^a }{\Gamma(a)}x^{a-1}e^{-bx}$

在本例中，令 a=2, b=1

$p(x) = Gamma(x,2,1)$

程式碼中， p_func 為 $p(x)$

而抽樣所用的 proposed distribution 為 exponantial distribution ：

$exp(x,\beta) = \frac{1}{\beta} e^{-\frac{x}{\beta}}$

在本例中，令 $\beta=5$

$q(x) = exp(x,5)$

此例的 $q(x)$ 跟上一時間點的 $x$ 值無關，即： $q(x_{t+1}) = q(x_{t+1}\mid x_{t})$ 。

程式碼中， q_func 和 q_func_pdf 為 $q(x)$ 。其中， q_func 用於產生 $a_j$ ，而 q_func_pdf 用於計算 correction factor 。

而進行 Metropolis Hasting 抽樣的演算法為程式碼中的 metrohast ，抽樣結果儲存於 X 。draw 則是將結果畫成 Histogram 。

用 metrohast 執行抽樣，並用 draw 畫出結果：

>>> X = metrohast(10000)
>>> draw(X)

結果如下：

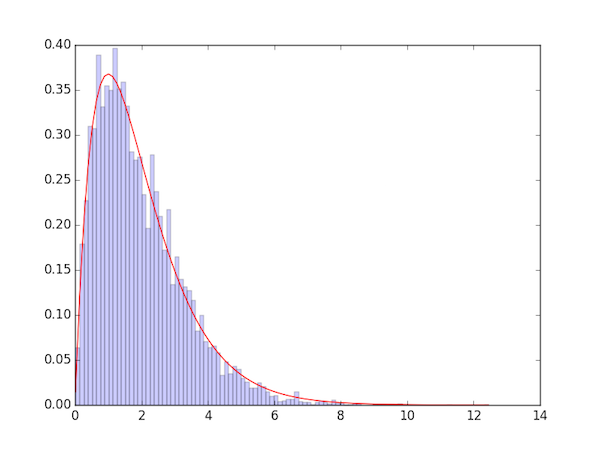
其中，紅色的線為 Gamma Distribution 實際上的值，藍色的線為 Metropolis Hasting 的抽樣結果。

Mark Chang's Blog

Machine Learning, Deep Learning and Python

Metropolis Hasting

Introduction

Metropolis Sampler