Gibbs Sampling

Introduction

Gibbs Sampling 是一種類似於 Metropolis Hasting 的抽樣方式，也是根據機率分佈來建立 Markov Chain ，並在 Markov Chain 上行走，抽樣出機率分佈。

設一 Markov Chain ，有 a 和 b 兩個 state ，它們的值分別為 $p(a)$ 和 $p(b)$ ，而它們之間的轉移機率，分別為 $q_1(a,b)$ 和 $q_2(a,b)$ ，如下圖：

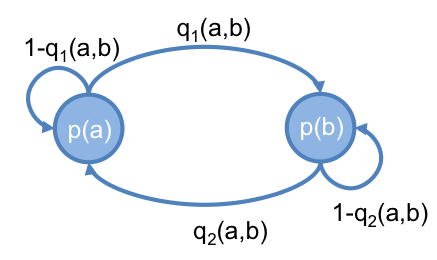
達平衡時，會滿足以下條件：

$\begin{align} & \begin{bmatrix} p(a) \\ p(b) \end{bmatrix} = \begin{bmatrix} 1-q_1(a,b) & q_2(a,b) \\ q_1(a,b) & 1-q_2(a,b) \end{bmatrix} \begin{bmatrix} p(a) \\ p(b) \end{bmatrix} \\ & \Rightarrow \begin{cases} p(a)(1-q_1(a,b) +p(b)q_2(a,b) = p(a) \\ p(a)q_1(a,b) + p(b)(1-q_2(a,b)) = p(b) \end{cases}\\ & \Rightarrow p(a)q_1(a,b) = p(b)q_2(a,b) \end{align}$

因此，達到平衡時，得出（公式一）：

$p(a)q_1(a,b) = p(b)q_2(a,b)$

在 Metropolis Hasting 這篇有提到，可以利用 Markov Chain 最終會達到平衡的特性，來為某機率分佈 $p(x)$ 抽樣。

但是 Metropolis Hasting 抽樣時，需要先用 proposed distribution 計算出下一個時間點可能的值，然後 acceptance probability 來拒絕它，因為計算出來的值會被拒絕，所以造成計算上的浪費。

而對於一高維度的機率分佈 $p(x_1,x_2,...,x_n)$ ，可以用另一種方式來建立 Markov Chain ，則不會有這個問題。這種方法為 Gibbs Sampling 。

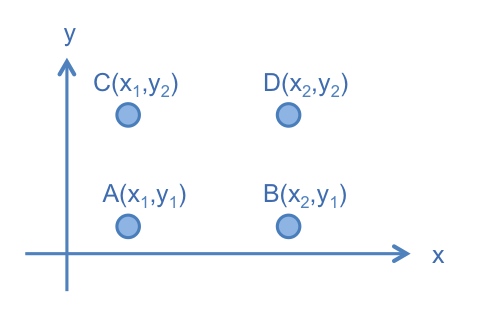
首先，先考慮二維的空間，設一機率分佈 $p(X,Y)$ ，若此機率分佈的 Random Variable 有四個值，分別為 $A(x_1,y_1)$ ， $B(x_2,y_1)$ ， $C(x_1,y_2)$ 和 $D(x_2,y_2)$ 。

首先，看看如何在 A 和 B 建立 Markov Chain 。由於 A 和 B 只有在 $x$ 維度上的值不一樣，則：

$\begin{align} & p(x_1,y_1)p(x_2|y_1)=p(y_1)p(x_1|y_1)p(x_2|y_1) \\ & p(x_2,y_1)p(x_1|y_1)=p(y_1)p(x_2|y_1)p(x_1|y_1) \end{align}$

由於兩式的等號右邊一樣，則可得出：

$\begin{align} p(x_1,y_1)p(x_2|y_1)=p(x_2,y_1)p(x_1|y_1) \end{align}$

此結果符合（公式一）的 Markov Chain 平衡狀態。根據此結果，建立以下的 Markov Chain ：

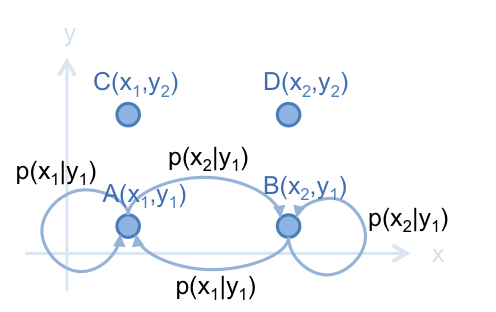
其中， $p(x_1\mid y_1)+p(x_2\mid y_1) = 1$ 。

若在此 Markov Chain 上行走，如果走得夠多次的話，走到 A 和走到 B 的次數比，會是 $p(x_1,y_1) : p(x_2,y_1)$ 。因此，用此 Markov Chain 得出的次數比，就相當於從機率分佈 $p(X,Y)$ 抽樣後， A 和 B 所抽出的次數比。

也可用同樣方法，在 A 和 C 之間建立 Markov Chain：

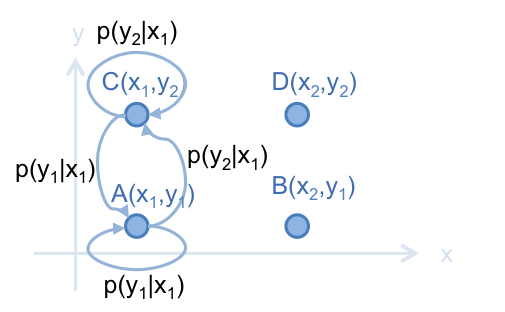
同理，D 和 B 或 C 之間，只有一個維度是不一樣的值，也可建立這樣的 Markov Chain 。

結合以上 Markov Chain ，若要對 $p(X,Y)$ 進行抽樣，則可先固定 $y$ 的值，先在 $x$ 軸上抽樣，再固定 $x$ 的值，在 $y$ 軸上抽樣，如此交替進行，即為 Gibbs Sampling 的方法。

舉個例子，假設有一聯合分佈 $p(X,Y)$ ，其機率值如下：

$\begin{array}{c | c c} p(X,Y) & Y=0 & Y=1 \\ \hline X=0 & 0.5 & 0.2 \\ X=1 & 0.1 & 0.2 \\ \end{array}$

這些點在座標上的位置如下圖：

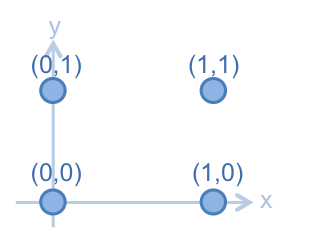
先把 $p(X\mid Y)$ 和 $p(Y\mid X)$ 計算出來，以便之後使用。

$\begin{align} & \begin{array}{c | c c} p(X|Y) & Y=0 & Y=1 \\ \hline X=0 & \frac{5}{6} & \frac{1}{2} \\ X=1 & \frac{1}{6} & \frac{1}{2} \\ \end{array} & \begin{array}{c | c c} p(Y|X) & Y=0 & Y=1 \\ \hline X=0 & \frac{5}{7} & \frac{2}{7} \\ X=1 & \frac{1}{3} & \frac{2}{3} \\ \end{array} \end{align}$

然後，進行 gibbs sampling ，首先，從 (0,0) 開始，固定 y 軸，在 x 軸上抽樣，用 $p(X\mid Y=0)$ 的值，建立從 (0,0) 在 x 軸上轉移的 Markov Chain ，如下：

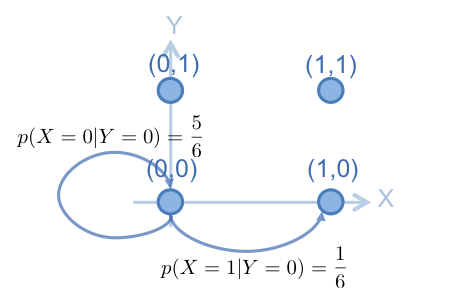
根據此 Marokv Chain ，從 $p(X\mid Y=0)$ 中，抽出 $X$ ，假設抽出的 $X$ 值為 1，則抽出來的點為 (1,0) ，下一步則是要固定 x 軸，在 y 軸上抽樣。用 $p(Y\mid Y=1)$ 的值，建立從 (1,0) 在 y 軸上轉移的 Markov Chain ，如下：

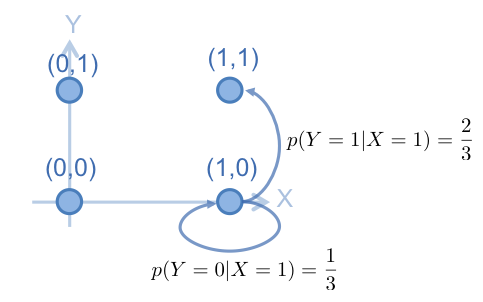
根據此 Marokv Chain ，從 $p(Y\mid X=1)$ 中，抽出 $Y$ ，假設抽出的 $Y$ 值為 1，則抽出來的點為 (1,1)，到目前為止，抽出來的樣本序列為這樣：

(0,0) (1,0) (1,1)

然後再固定 y 軸，在 x 軸上抽樣，這樣持續抽樣下去，抽到最後，得出以下序列：

(0,0) (1,0) (1,1) (0,1) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (1,0)
(1,1) (1,1) (1,1) (1,1) (1,0) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0)
(0,1) (1,1) (1,1) (0,1) (0,1) (0,1) (0,0) (0,0) ...

最後，統計抽樣序列中各個點的出現次數， (0,0) (1,0) (1,1) (0,1) 這四個點的次數比會接近 0.5 : 0.1 : 0.2 : 0.2

Gibbs Sampling 也可用在高維度的機率分佈 $p(x_1,x_2,...,x_n)$ 。抽樣時，先從第一個維度上抽樣，固定其他維度，用 $p(x_1\mid x_2,...,x_{n})$ 抽出下一個樣本，然後再從第二個維度抽樣，固定其他維度，用 $p(x_2\mid x_1,x_3,...,x_{n})$ 抽出下一個樣本，如此一直循環下去。

整個抽樣過程的 pseudo code 如下：

$\begin{align} 1 & \text{set }t = 0 \\ 2 & \text{generate an initial state } \textbf{x}_0 \in \text{domain of }p(x_1,x_2,...,x_n) \\ 3 & \text{repeat until }t = M \\ 4 & \mspace{30mu}\text{for each dimension }i = 1...n \\ 5 & \mspace{60mu}\text{draw } \textbf{x}_t \text{ from } p(x_i|x_1,x_2,\dots,x_{i-1},x_{i+1},\dots,x_n) \\ 6 & \mspace{60mu}\text{set }t = t+1 \end{align}$

此處流程大致上和 Metropolis Hasting 類似，而 $p(x_i\mid x_1,x_2,\dots,x_{i-1},x_{i+1},\dots,x_n)$ 就相當於是 Metropolis Hasting 中的 proposed distribution ，但在 Gibbs Sampling 中， $p(x_i\mid x_1,x_2,\dots,x_{i-1},x_{i+1},\dots,x_n)$ 得出的值，就直接是抽樣結果了，不需要再算一個 acceptance probability 來判斷是否要接受或拒絕它。因此，不會造成計算上的浪費。

Implementation

此例實作先前提到的 $p(X,Y)$ 抽樣：

$\begin{array}{c | c c} p(X,Y) & Y=0 & Y=1 \\ \hline X=0 & 0.5 & 0.2 \\ X=1 & 0.1 & 0.2 \\ \end{array}$

程式碼如下：

gibbssamp.py

import numpy as np
from collections import Counter

def gibbssamp(m):
    P = np.matrix([[0.5, 0.2], [0.1, 0.2]])
    condi = [np.divide(P, np.sum(P, axis=0)), np.divide(P, np.sum(P, axis=1)).T]
    x = [0, 0]
    samples = []
    for i in range(m):
        for j in range(2):
            one_prob = condi[j][1, x[(j + 1) % 2]]
            x[j] = np.random.binomial(1, one_prob, 1)[0]
            samples.append([x[0], x[1]])
    return samples


def count(samples):
    c = Counter()
    for s in samples:
        c.update(["(%s,%s)" % (s[0], s[1])])
    for k in c.keys():
        print k, c[k]

其中，程式碼中的 P 為機率分佈 $p(X,Y)$ ， condi[0] 為 $p(X\mid Y)$ ， condi[1] 為 $p(Y\mid X)$ 。 gibbssamp 為執行 Gibbs Sampling 的主要函數。

執行 gibbssamp 抽出 1000 * 2 個樣本，如下：

>>> X = gibbssamp(1000)
>>> print X
[[0, 0], [0, 0], [1, 0], [1, 1], [0, 1], [0, 1], [0, 1], [0, 0], [0, 0], [0, 0], [0, 0], [0, 1],
[0, 1], [0, 1], [0, 1], [0, 1], [1, 1], [1, 1], [0, 1], [0, 0], [0, 0], [0, 1], [1, 1], [1, 1],
[1, 1], [1, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [1, 0], [1, 1],
[0, 1], [0, 1], [0, 1], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0],
[0, 0], [0, 0], [1, 0], [1, 1], [1, 1], [1, 0], [0, 0], [0, 1], [0, 1] ...

用 count 用來統計抽樣結果：

>>> count(X)
(0,0) 1043
(1,0) 172
(0,1) 387
(1,1) 398

統計結果顯示， (0,0) (1,0) (0,1) (1,1) 的比率會接近 0.5 : 0.1 : 0.2 : 0.2

Mark Chang's Blog

Machine Learning, Deep Learning and Python

Gibbs Sampling

Introduction

Gibbs Sampling

Implementation

Further Reading

Comments