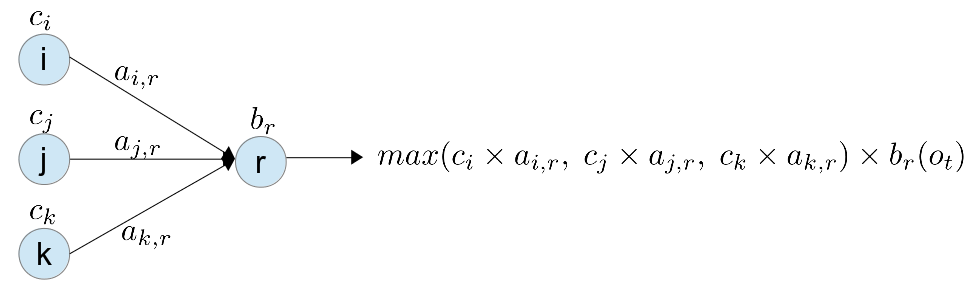Viterbi Algorithm

1.Introduction

本文接續先前提到的 Hidden Markov Model

Natural Language Processing – Hidden Markov Model

繼續探討 part of speech tagging 的演算法

先前提到, 如果要在 Hidden Markov Model 找出一個機率最大的 tagging sequence

則必須把每一個序列都列出來, 看哪一個是機率最大的

但如果 Tag 有 $N$ 種, 那麼長度為 $T$ 的序列, 就有 $N^{T}$ 種可能的 tagging sequence

由此可知, 暴力列舉的演算法非常沒有效率

2.Viterbi Algorithm

那麼, 來看看暴力列舉法, 到底出了什麼問題

在計算這些序列的機率時, 假設目前已經計算到了第 $t$ 個字 $o_{t}$ , 這個字的 tag 為 $r$ 時, 上一個字的 tag 為 $s$ , 則此種情況發生的機率為

$P(q_{t}=r \mid q_{t-1} = s)\times P(X_{t}=o_{t} \mid q_{t} = r)=a_{s,r}\times b_{r}(o_{t}),\mspace{10mu} s \in {i,j,k}$

其中, $s$ 有三種可能, 分別是 $i$ , $j$ , $k$

假設在 $t-1$ 之前的序列為 $C_{i} , C_{j} , C_{k}$ ,且在 $i,j,k$ 這三個 state 的機率分別為 $c_{i} , c_{j} , c_{k}$

若是使用暴力列舉法, 要分別計算 $C_{i}ir$ , $C_{j}jr$ , $C_{k}kr$ 這三個序列的機率, 如下圖

viterbi1

由上圖可知 , 在 $r$ 這個 state ,就多增加了 3 個序列傳遞下去, 之後每個 state 都會因為前面有 N 種不同的 state , 而增加 N 種不同的序列, 這樣一直增加, 序列的數量呈指數函數成長, 最後再一起比誰的機率比較大

這就是造成暴力列舉法沒效率的原因

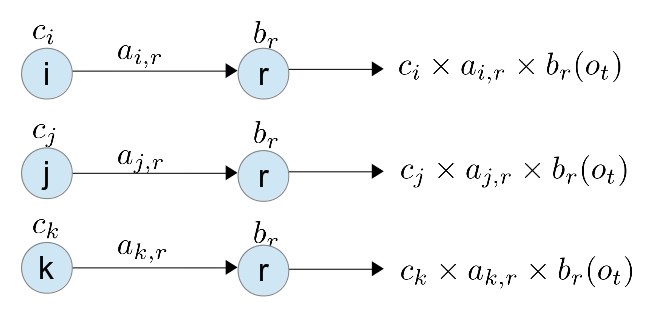
其實, 可以用 Dynamic Programming 的概念, 在計算每個 state 的機率時, 就直接比較序列的機率大小,

只保留機率最大的一條序列, 傳遞下去, 如下圖

viterbi2

這樣每一個 state 就只會傳遞一個序列下去, 不會使序列數量呈指數成長

這就是所謂的 Viterbi Algorithm

3.Example

舉個例子,

有個研究者, 想根據某地人們生活日記中, 記載每天吃冰淇淋的數量, 來推斷當時的天氣變化如何

在某個地點有兩種天氣, 分別是 Hot 和 Cold , 而當地的人們會記錄他們每天吃冰淇淋的數量, 數量分別為 1 , 2 或 3 ,

則可以把天氣變化的機率, 以及天氣吃冰淇淋數量的關係, 用 Hidden Markov Model 表示,

由於天氣是未知的, 為 hidden state , 天氣的集合為 $Weather=\{HOT,COLD\}$

而冰淇淋數量是已知的, 為 observable , 冰淇淋數量的集合為 $Icecream=\{1,2,3\}$

天氣的 Transition Matrix , $A$ , 以及天氣變化對於冰淇淋數量的 Output Matrix , $B$ 如下

$A:\begin{array}{c|c} _{Day_{t}}\setminus _{Day_{t+1}} & HOT & COLD \\\hline \hline HOT & 0.7 & 0.3 \\ \hline COLD & 0.4 & 0.6 \\ \end{array}\mspace{50mu} B:\begin{array}{c|c} _{Weather}\setminus _{Icecream} & 1 & 2 & 3 \\\hline \hline HOT & 0.2 & 0.4 & 0.4 \\ \hline COLD & 0.5 & 0.4 & 0.1\\ \end{array}$

如果冰淇淋的記錄 $(3,1,1)$ , 用 Viterbi Algorithm 計算看看可能的天氣序列是什麼

首先, 從 initial state 開始, 計算第一個 state 是 $H$ 以及 $C$ 的機率

$\begin{align} &P(X_{1}=3 , q_{1} = H) = P(q_{1}=H)\times P(X_{1}=3 \mid q_{1} = H) = 0.8 \times 0.4 = 0.32 \\ &P(X_{1}=3 , q_{1} = C) = P(q_{1}=C)\times P(X_{1}=3 \mid q_{1} = C) = 0.2 \times 0.1 = 0.02 \end{align}$

計算結果如下圖

再來, 我們來計算第二個 state 是 $H$ 的機率, 我們分別要算序列 $CH$ 和 $HH$ 的序列

$\begin{align} & P(X_{1}=3 , q_{1} = H) \times P(q_{2}=H \mid q_{1}=H)\times P(X_{2}=1 \ mid q_{2} = H) =0.32 \times 0.7 \times 0.2 = 0.0448 \\ & P(X_{1}=3 , q_{1} = C) \times P(q_{2}=H \mid q_{1}=C)\times P(X_{2}=1 \ mid q_{2} = H) =0.02 \times 0.4 \times 0.2 = 0.0016 \end{align}$

結果如下圖：

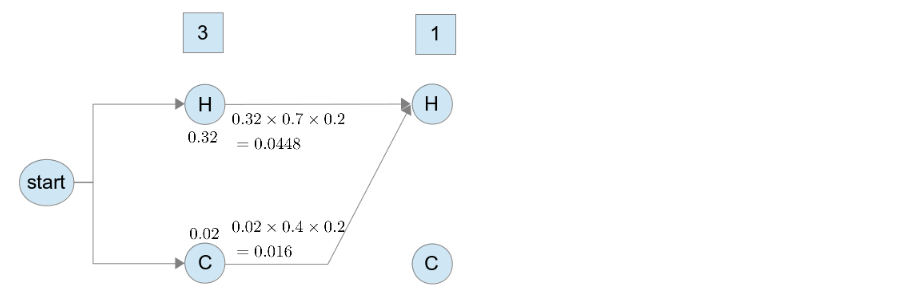
用 Viterbi Algorithm , 在同一個 state 只需要保留機率最大的序列即可

$max( 0.0448, 0.0016 ) = 0.0448$

因此我們在 state $H$ 上, 只需要保留機率為 $0.048$ 的序列 $HH$ , 傳遞下去, 如下圖

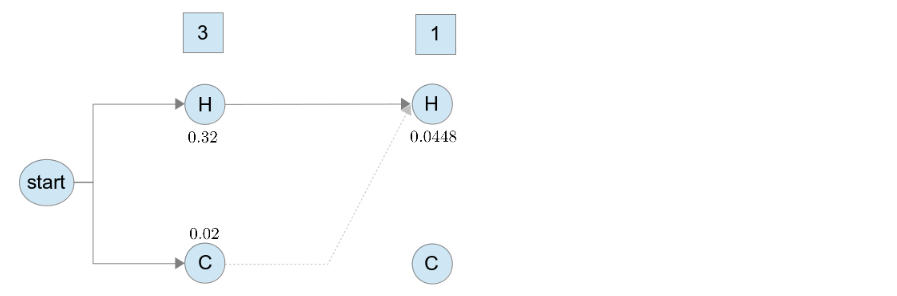
就用這樣的概念, 之後的每一個 state 都這樣計算, 就會得到每個 state 的機率值, 如下圖

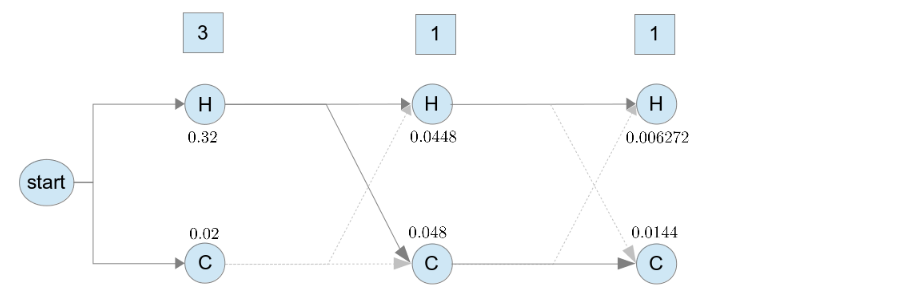
全部算完後, 再比較序列的最後一個 state, 哪一個機率比較大, 較大者可以傳遞到 end state (也就是最後的答案)

然後, 從 end state 回溯之前保留下來的序列, 如下圖

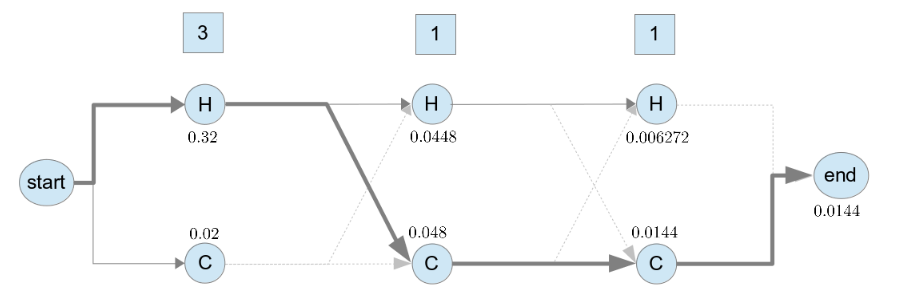
得出最有可能的序列是 HCC

動畫版：

4.Implementation

接著我們來實作一下, 先前提到的暴力列舉法, 以及 Viterbi 演算法

並比較這兩者的performance差異

新增一個python script檔案, 檔名為 viterbi.py ,並加入以下程式碼

1.前例中的Model, 和必要模組

viterbi.py

import timeit
_STATE=['H','C']
_PI={'H':.8, 'C':.2}
_A={ 'H':{'H':.7, 'C':.3 }, 'C':{'H':.4,'C':.6} }
_B={'H':{1:.2,2:.4,3:.4}, 'C':{1:.5,2:.4,3:.1} }

def p_aij(i, j):
    return _A[i][j]

def p_bik(i, k):
    return _B[i][k]

def p_pi(i):
    return _PI[i]

其中, timeit 是用來計時的模組, 用於比較演算法所花的時間,

而 _STATE , _PI 是 state 的種類和 initial state 的機率,

_A 和 _B 是 Transition Matrix 和 *Output Matrix’,

p_aij(i, j) , p_bik(i, k) , p_pi(i) 分別是 $P(q_{t+1} = j \mid q_{t} = i)$ , $P(X_{t} = k , q_{t} = i)$ 和 $\pi_{i}$

2.暴力列舉法的function: brute_force_algo(obs_init, print_seq=False)

viterbi.py

def brute_force_algo(obs_init, print_seq=False):
    start = timeit.default_timer()
    seq_val=[];
    def rec(obs, val_pre, qseq_pre):
        if len(obs) >0:
            for q in _STATE:
                if len(qseq_pre) == 0 :
                    val = val_pre * p_pi(q) * p_bik(q, obs[0])
                else:
                    q_pre = qseq_pre[-1]
                    val = val_pre * p_aij(q_pre,q) * p_bik(q, obs[0])
                qseq = qseq_pre + [q]
                rec(obs[1:], val, qseq)
        else:
            seq_val.append((qseq_pre, val_pre))
    rec(obs_init, 1, [])
    if print_seq:
        for (seq,val) in seq_val:
            print 'seq : %s , value : %s'%(seq, val)
    print 'result of brute_force_algo:'
    stop = timeit.default_timer()
    print 'max_seq : %s  max_val : %s'%(
          reduce(lambda x1,x2: x2 if x2[1] > x1[1] else x1, seq_val))
    print 'runtime : %s'%(stop - start )

其中, input argument obs_init 是 observable ,

print_seq 是用來控制是否要印出計算過程中產生的序列, 或者只印出最後結果

演算法用 recursive function 的方式實現, 詳細內容在此不詳述,

3.viterbi演算法的function: viterbi_algo(obs_init, print_seq=False)

viterbi.py

def viterbi_algo(obs_init, print_seq=False):
    start = timeit.default_timer()
    state_snapshot=[]
    def rec(obs, val_pre, qseq_pre):
        if len(obs) > 0:
            val = {}
            qseq = {}
            for q in _STATE:
                if len(val_pre) == 0:
                    val.update({ q:p_pi(q) * p_bik(q, obs[0]) })
                    qseq.update({q:[]})
                    state_snapshot.append(([q],val[q]))
                else:
                    val_temp = [( qseq_pre[q_pre]+[q_pre],
                                val_pre[q_pre] * p_aij(q_pre,q) * p_bik(q, obs[0] ))
                                for q_pre in _STATE ]
                    max_q_seq = reduce(lambda x1,x2: x2 if x2[1] > x1[1] else x1, val_temp)
                    state_snapshot.append((max_q_seq[0]+[q],max_q_seq[1]))
                    val.update({ q:max_q_seq[1]  })
                    qseq.update({ q:max_q_seq[0] })
            return rec(obs[1:],val,qseq)
        else:
            val_temp =[( qseq_pre[q]+[q] , val_pre[q] ) for q in _STATE ]
            max_q_seq = reduce(lambda x1,x2: x2 if x2[1] > x1[1] else x1, val_temp)
            return max_q_seq
    seq,val = rec(obs_init, {},[])
    if print_seq:
        for (seq,val) in state_snapshot:
            print 'seq : %s , value : %s'%(seq, val)
    print 'result of viterbi_algo:'
    print 'max_seq : %s , max_value : %s'%(seq, val)
    stop = timeit.default_timer()
    print 'runtime : %s'%(stop - start )

其中, 所使用的參數, 和暴力列舉法一樣

唯演算法部份改用 Viterbi algorithm , 但也是以 recursive function 的形式寫成, 在此不詳述

接著到interactive mode 載入 viterbi.py

>>> import viterbi

先來看一下暴力列舉法

>>> viterbi.brute_force_algo([3,1,1],True)
seq : ['H', 'H', 'H'] , value : 0.006272
seq : ['H', 'H', 'C'] , value : 0.00672
seq : ['H', 'C', 'H'] , value : 0.00384
seq : ['H', 'C', 'C'] , value : 0.0144
seq : ['C', 'H', 'H'] , value : 0.000224
seq : ['C', 'H', 'C'] , value : 0.00024
seq : ['C', 'C', 'H'] , value : 0.00048
seq : ['C', 'C', 'C'] , value : 0.0018
result of brute_force_algo:
max_seq : ['H', 'C', 'C']  max_val : 0.0144
runtime : 0.000172138214111

暴力列舉法會列出所有的序列, 並找出機率最大的序列

再來是 viterbi algorithm

>>> viterbi.viterbi_algo([3,1,1],True)
seq : ['H'] , value : 0.32
seq : ['C'] , value : 0.02
seq : ['H', 'H'] , value : 0.0448
seq : ['H', 'C'] , value : 0.048
seq : ['H', 'H', 'H'] , value : 0.006272
seq : ['H', 'C', 'C'] , value : 0.0144
result of viterbi_algo:
max_seq : ['H', 'C', 'C'] , max_value : 0.0144
runtime : 0.000169038772583

Viterbi algorithm 不會把每個序列都列出來, 而是用 Dynamic Programming 的方式, 保留下比較有可能的 subsequence , 最後也可以得出正確結果 , 且runtime比暴力列舉法快

再來, 增加一下input sequence的長度, 讓這兩種演算法的差異突顯出來,

為了避免印出過多序列, 第二個參數輸入 False , 如下

>>> viterbi.brute_force_algo([3,1,1,2]*4,False)
result of brute_force_algo:
max_seq : ['H', 'C', 'C', 'H', 'H', 'C', 'C', 'H', 'H', 'C', 'C', 'H', 'H', 'C', 'C', 'C']  max_val : 2.83168745718e-11
runtime : 0.245212078094

>>> viterbi.viterbi_algo([3,1,1,2]*4,False)
result of viterbi_algo:
max_seq : ['H', 'C', 'C', 'H', 'H', 'C', 'C', 'H', 'H', 'C', 'C', 'H', 'H', 'C', 'C', 'C'] , max_value : 2.83168745718e-11
runtime : 0.000442981719971

比較一下, 暴力列舉法的 runtime 呈指數函數成長, 而 viterbi algorithm 的是呈多項式函數成長

5. Reference

本文參考至兩本教科書

Foundations of Statistical Natural Language Processing

Speech and Language Processing

以及台大資工系陳信希教授的自然語言處理課程講義

Mark Chang's Blog

Machine Learning, Deep Learning and Python

1.Introduction

2.Viterbi Algorithm

3.Example

4.Implementation

5. Reference

Comments