Hidden Markov Model

1.Markov Model

Hidden Markov Model 在 natural language processing 中,

常用於 part-of speech tagging

想要了解 Hidden Markov Model ,就要先了解什麼是 Markov Model

例如, 可以把語料庫中,各種字串的機率分佈,

看成是一個Random varaible 的 sequence , $X=(X_{1},X_{2},...,X_{T})$

其中, $X$ 的值是 alphabet (字)的集合 : $S=\{s_{1},s_{2},...,s_{n}\}$

如果想要知道一個字串出現的機率, 則可以把字串拆解成Bigram, 逐一用前一個字,來推估下一個字的機率是多少

但是要先假設以下的 Markov Assumption

$\begin{align*} &\text{Limited Horizon : } P(X_{t+1} = s_{k} \mid X_{1},...,X_{t} ) = P(X_{t+1} = s_{k} \mid X_{t} ) \\ &\text{Time Invariant : } P(X_{t+1} = s_{k} \mid X_{t} ) = P(X_{2} = s_{k} \mid X_{1}) \end{align*}$

其中,

Limited Horizon 的意思是,

每個 $X_{t+1}$ 是什麼字 $(s_{i})$ 的機率, 只會受到上一個字 $X_{t}$ 的影響

Time Invariant 的意思是,

每個 $X_{t+1}$ 是什麼字 $(s_{i})$ 的機率, 和前一個字 $X_{t}$ 的機率關係, 不會因為在字串中的位置不同, 而有所改變

註：事實上, 這兩種假設是為了簡化計算, 在真實的自然語言中, 以上兩種假設都不成立

做完以上兩個假設之後,

再用語料庫, 把上一個字是 $s_{i}$ 時, 這個字是 $s_{j}$ 的機率, 建立成 Transition Matrix : $A$ , 則 $A$ 中的元素可以寫成：

$a_{i,j} = P(X_{t+1} =s_{j} \mid X_{t}=s_{i})$

也可以用 Transition Diagram 來表示：

hmm1

如果想要計算字串 $(s_{1},s_{2},...,s_{T})$ 在 Model 中出現的機率, 可以從第一個字開始, 用 Transition Matrix 逐字推算下去

設 Initial State (第一個字）的機率, $P(X_{1} = s_{1} )=\pi_{s_{1}}$ , 則 Random sequence, $(X_{1},X_{2},...,X_{T})$ ,的機率為：

$\begin{align} &P(X_{1} = s_{1} ,X_{2} = s_{2} ,...,X_{T} = s_{T}) \\[6pt] &=P(X_{1}= s_{1})P(X_{2}= s_{s}\mid X_{1}= s_{1})...P(X_{T}= s_{T}\mid X_{T-1}= s_{T-1}) \\[6pt] &=\pi_{s_{1}} \prod_{t=2}^{T} P(X_{t}= s_{t}\mid X_{t-1}= s_{t-1}) \\[6pt] &=\pi_{s_{1}} \prod_{t=2}^{T} a_{X_{t},X_{t+1}} \end{align}$

舉個例子

假設有個 Markov Model,

alphabet 的集合為 $S=\{ 0, 1 \}$

Initial State 的機率為 $\pi_{0}=0.2,\pi_{1}=0.8$

Transition Matrix 為

$\begin{array}{c|c} _{X_{t}}\setminus _{X_{t+1}} & 0 & 1 \\\hline \hline 0 & 0.3 & 0.7 \\ \hline 1 & 0.6 & 0.4 \\ \end{array}$

用 Transition Diagram 表示成：

hmm2

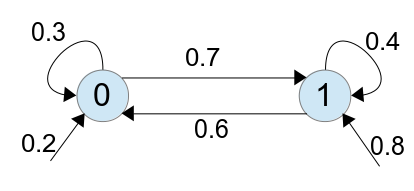
則在此 Model 中, 出現字串 1011 的機率為：

$\begin{align} &P(X_{1}=1,X_{2}=0,X_{3}=1,X_{4}=1) \\[6pt] &=\pi_{1} \times P(X_{2}= 0 \mid X_{1} = 1) \times P(X_{3}= 1 \mid X_{2} = 0) \times P(X_{4}= 1 \mid X_{3} = 1) \\[6pt] &= 0.8 \times 0.6 \times 0.7 \times 0.4 \\[6pt] &= 0.1344 \end{align}$

2.Hidden Markov Model

所謂的 Hidden Markov Model , 就是從表面上看不到 state 是什麼

例如在做 part-of speech tagging 的時候, tag 為 state, 不知道哪個字要給哪個 tag

只能看到表面上的字, 從 words(observable) 去推斷 tag(hidden state) 是什麼

其中, observable 為一個集合 : $O=\{o_{1},o_{2},...,o_{n}\}$

hidden state 為一集合 : $Q=\{q_{1},q_{2},...,q_{n}\}$

則表示當某個字的 tag 為 $i$ 時, 這個字為 $o_{k}$ 的機率, 可用 Output Matrix : $B$ 表示, 則` $B$ $ 中的元素可以寫成：

$b_{i}(o_{k})=P(X_{t}=o_{k} \mid q_{t} = i)$

則當上一個 tag 為 $j$ 時, 這個字的 tag 為 $i$ 的機率為：

$a_{j,i} = P(q_{t} =i \mid q_{t-1}=j)$

則我們可以算在上一個 tag 為 $j$ 時, 這個字的 tag 為 $i$ , 且這個字為 $o_{k}$ 的機率：

$\begin{align} &P(q_{t} =i \mid q_{t-1}=j) (X_{t}=o_{k} \mid q_{t} = i) \\ &= a_{j,i} \times b_{i}(k) \\ \end{align}$

如果我們要計算, 出現字串 $(o_{1},o_{2},...,o_{T})$ 且 tag 為 $(r_{1},r_{2},...,r_{T})$ 的機率:

$\begin{align} &P(X_{1} = o_{1} ,X_{2} = o_{2} ,...,X_{T} = o_{T}, q_{1}=r_{1},q_{2}=r_{2},...,q_{T}=r_{T}) \\[6pt] &= P(q_{1}= r_{1}) P(X_{1}=o_{1} \mid q_{1} = r_{1} ) \times P(q_{2} =r_{2} \mid q_{1}=r_{1}) P(X_{2}= o_{2} \mid q_{2} = r_{2} ) \times... \\ & \times P(q_{T} =r_{T} \mid q_{T-1}=r_{T-1}) P(X_{T}= o_{T} \mid q_{T} = r_{T} ) \\[6pt] &=\pi_{r_{1}} P(X_{1}=o_{1} \mid q_{1} = r_{1} ) \prod_{t=2}^{T} P(q_{t} =r_{t} \mid q_{t-1}=r_{t-1}) P(X_{t}= o_{t} \mid q_{t} = r_{t} ) \\[6pt] &=\pi_{r_{1}} b_{r_{1}}(o_{1}) \prod_{t=2}^{T} a_{r_{t-1},r_{t}} b_{r_{t}}(o_{t}) \end{align}$

如果要求出這個字串最有可能個 tag ,

則找出 $r$ 的序列, 可以讓 $P(X_{1} = o_{1} ,X_{2} = o_{2} ,...,X_{T} = o_{T}, q_{1}=r_{1},q_{2}=r_{2},...,q_{T}=r_{T})$ 為最大值

$\mathop{\arg\,\max}\limits_{r_{i},r_{m},r_{n} \in Q} \pi_{r_{i}} b_{r_{i}}(o_{1}) \prod_{t=2}^{T} a_{ r_{n} , r_{m} } b_{r_{m}}(o_{k})$

舉個例子,

有個研究者, 想根據某地人們生活日記中, 記載每天吃冰淇淋的數量, 來推斷當時的天氣變化如何

在某個地點有兩種天氣, 分別是 Hot 和 Cold , 而當地的人們會記錄他們每天吃冰淇淋的數量, 數量分別為 1 , 2 或 3 ,

則可以把天氣變化的機率, 以及天氣吃冰淇淋數量的關係, 用 Hidden Markov Model 表示,

由於天氣是未知的, 為 hidden state , 天氣的集合為 $Weather=\{HOT,COLD\}$

天氣的 Transition Matrix :

$\begin{array}{c|c} _{Day_{t}}\setminus _{Day_{t+1}} & HOT & COLD \\\hline \hline HOT & 0.7 & 0.3 \\ \hline COLD & 0.4 & 0.6 \\ \end{array}$

而冰淇淋數量是已知的, 為 observable , 冰淇淋數量的集合為 $Icecream=\{1,2,3\}$

天氣變化對於冰淇淋數量的 Output Matrix :

$\begin{array}{c|c} _{Weather}\setminus _{Icecream} & 1 & 2 & 3 \\\hline \hline HOT & 0.2 & 0.4 & 0.4 \\ \hline COLD & 0.5 & 0.4 & 0.1\\ \end{array}$

而 Initial State 的機率為 $\pi_{HOT}=0.8, \pi_{COLD}=0.2$

根據這個 Model , 假設有個吃冰淇淋的記錄 $(3,1,3)$ , 想要預測當時的天氣如何,

例如, 出現天氣序列為 HCH 且冰淇淋的記錄為 $(3,1,3)$ 的機率如下

$\begin{align} &P (X_{1} = 3 ,X_{2} = 1 ,X_{3} = 3 , q_{1}=H , q_{2}= C, q_{3}=H ) \\[6pt] &=P(q_{1}=H)P(X_{1}=3 \mid q_{1}=H) \times P(q_{2}=C \mid q_{1}=H ) P(X_{2}=1 \mid q_{2}=C)\\ &\times P(q_{3}=H \mid q_{2}=C) P(X_{3}=3 \mid q_{3}=H) \\[6pt] &=0.8 \times 0.4 \times 0.3 \times 0.5 \times 0.4 \times 0.4 \\[6pt] &=0.00768 \end{align}$

如果有冰淇淋的記錄 $(3,1,3)$ , 但不知道當時天氣如何, 想要預測當時的天氣如何,

可以把所有可能的天氣序列都列出來：

HHH HHC HCH HCC CHH CHC CCH CCC

然後分別計算, 哪個天氣序列和冰淇淋的記錄為 $(3,1,3)$ 共同發生的機率, 看看哪個機率最高

3.Implementation

接著來實作 Hidden Markov Model

根據上一個例子, 建立出以下的 Model 以及演算法

hmm.py

_STATE=['H','C']
_PI={'H':.8, 'C':.2}
_A={ 'H':{'H':.7, 'C':.3 }, 'C':{'H':.4,'C':.6} }
_B={'H':{1:.2,2:.4,3:.4}, 'C':{1:.5,2:.4,3:.1} }

def p_aij(i, j):
    return _A[i][j]

def p_bik(i, k):
    return _B[i][k]

def p_pi(i):
    return _PI[i]

def seq_probability(obs_init):
    seq_val=[];
    def rec(obs, val_pre, qseq_pre):
        if len(obs) >0:
            for q in _STATE:
                if len(qseq_pre) == 0 :
                    val = val_pre * p_pi(q) * p_bik(q, obs[0])
                else:
                    q_pre = qseq_pre[-1]
                    val = val_pre * p_aij(q_pre,q) * p_bik(q, obs[0])
                qseq = qseq_pre + [q]
                rec(obs[1:], val, qseq)
        else:
            seq_val.append((qseq_pre, val_pre))
    rec(obs_init, 1, [])
    for (seq,val) in seq_val:
        print 'seq : %s , value : %s'%(seq, val)
    print 'max_seq : %s  max_val : %s'%( reduce(lambda x1,x2: x2 if x2[1] > x1[1] else x1, seq_val))

其中,

_STATE=['H','C'] 是天氣的種類

_PI={'H':.8, 'C':.2} 是 initial state 的機率

_A={ 'H':{'H':.7, 'C':.3 }, 'C':{'H':.4,'C':.6} } 是 Transition Matrix

_B={'H':{1:.2,2:.4,3:.4}, 'C':{1:.5,2:.4,3:.1} } 是 Output Matrix

p_aij(i, j) , p_bik(i, k) , p_pi(i) 是 Model 和演算法的interface

seq_probability(obs_init) 是計算 sequence probability 的演算法

這個演算法,會根據 observable 把每種天氣序列的機率都算出來, 並求出最有可能的序列是哪個

接著到interactive mode試看看剛剛的例子

輸入了冰淇淋的記錄 $(3,1,3)$ , 程式會把每種可能的天氣序列都列出來, 並求得最有可能者, 如下：

hmm.py

>>> import hmm
>>> hmm.seq_probability([3,1,3])
seq : ['H', 'H', 'H'] , value : 0.012544
seq : ['H', 'H', 'C'] , value : 0.001344
seq : ['H', 'C', 'H'] , value : 0.00768
seq : ['H', 'C', 'C'] , value : 0.00288
seq : ['C', 'H', 'H'] , value : 0.000448
seq : ['C', 'H', 'C'] , value : 4.8e-05
seq : ['C', 'C', 'H'] , value : 0.00096
seq : ['C', 'C', 'C'] , value : 0.00036
max_seq : ['H', 'H', 'H']  max_val : 0.012544

程式算出答案, 最有可能的序列為 ['H', 'H', 'H'] ,機率為 0.012544

其實, 把所有的序列都列出來, 這樣的演算法是非常沒有效率的

假設序列長度為 $T$ , state 有 $N$ 種, 則所有可能的序列有 $N^{T}$ 種

事實上, 我們要求機率最高的序列, 不需要把所有的序列都算出來, 用 Dynamic Programming 的技巧, 就可以了,

有一種演算法, 叫 Viterbi Algorithm 是將 Dynamic Programming 應用於 Hidden Markov Model

想知道什麼是 Viterbi Algorithm , 請看：Natural Language Processing – Viterbi Algorithm

4. Reference

本文參考至兩本教科書

Foundations of Statistical Natural Language Processing

Speech and Language Processing

以及台大資工系陳信希教授的自然語言處理課程講義

Mark Chang's Blog

Machine Learning, Deep Learning and Python

1.Markov Model

2.Hidden Markov Model

3.Implementation

4. Reference

Comments