Introduction

在解「 有條件的最佳化問題 」時，有時需要把原本的問題轉換成對偶問題(Dual Problem)後，會比較好解。

如果對偶問題有最佳解，原本問題也有最佳解，且這兩個最佳解相同，則必須要滿足 Karush-Kuhn-Tucker (KKT) Conditions：

1. Primal Feasibility

2. Dual Feasibility

3. Complementary Slackness

4. Stationarity

至於這四項到底是什麼？講起來有點複雜。本文會先從對偶問題的概念開始介紹，再來講解這四個條件。

The Lagrange dual function

首先，講解一下什麼是對偶問題。

通常，有條件的最佳化問題，可寫成 ＜公式一＞ ：

$$\begin{aligned} & \textbf{minimize} & f_{0}(x) & \\ & \textbf{subject to } & f_{i}(x) \leq 0 ,& i=1, ... ,m \\ & & h_{j}(x) = 0 , &j=1, ... ,p \\ \end{aligned}$$

其中, $f_{0}(x)$ 是目標函數，而 $f_{i}(x) \leq 0$ 為不等式的條件限制， $h_{j}(x) = 0$ 為等式的條件限制。也就是說，最佳化的目標是要求出 $x$ 讓 $f_{0}(x)$ 得出最小值，而這個 $x$ ，必須滿足 $f_{i}(x) \leq 0$ 和 $h_{j}(x) = 0$ 所限定的條件。若滿足這兩項條件，則表示這個最佳化問題有解，即為滿足 primal feasibility 。

此最佳化問題可以轉換成對偶問題，如下：

$$L(x, \lambda, \nu) = f_{0}(x) + \sum_{i=1}^{m} \lambda_{i} f_{i}(x) + \sum_{j=1}^{p} \nu_{j} h_{j}(x)$$

其中，我們把 $L(x, \lambda, \nu)$ 稱為 Lagrangian ，$\lambda_{i}$ 和 $\nu_{j}$ 稱為 Lagrange multiplier 。

所謂的對偶函數( Lagrange dual function )，即是在給定了 Lagrange multiplier 之下，改變 $x$ 來得出 Lagrangian 最小值，如下：

$$g(\lambda, \nu) = \inf_{x}( L(x, \lambda, \nu) ) = \inf_{x}( f_{0}(x) + \sum_{i=1}^{m} \lambda_{i} f_{i}(x) + \sum_{j=1}^{p} \nu_{j} h_{j}(x) )$$

其中， $g(\lambda, \nu)$ 為對偶函數，而 $\inf_{x}$ 即是在改變 $x$ 的情況下，找出最小值。

Lower bounds on optimal value

接著來證明，對偶函數可當作原本問題的 Lower Bound 。設原本問題公式一的最佳解為 $p^{\star}$ ，則在所有 $\lambda_{i} \geq 0$ （記作 $\lambda \succeq 0$ ）和 $\nu_{j}$ 為任意數的情況下，會滿足以下條件：

$$g(\lambda, \nu) \leq p^{\star}$$

此性質不難證明，對於所有滿足 $f_{i}(\tilde{x}) \leq 0$ 和 $h_{j}(\tilde{x}) = 0$ 這兩個條件的 $\tilde{x}$ ，必滿足：

$$\sum_{i=1}^{m} \lambda_{i} f_{i}(\tilde{x}) + \sum_{j=1}^{p} \nu_{j} h_{j}(\tilde{x}) \leq 0$$

則：

$$\begin{aligned} & g(\lambda, \nu) = \inf_{x}( L(x, \lambda, \nu) ) = \inf_{x}( f_{0}(x) + \sum_{i=1}^{m} \lambda_{i} f_{i}(x) + \sum_{j=1}^{p} \nu_{j} h_{j}(x) ) \\ & \leq L(\tilde{x}, \lambda, \nu) = f_{0}(\tilde{x}) + \sum_{i=1}^{m} \lambda_{i} f_{i}(\tilde{x}) + \sum_{j=1}^{p} \nu_{j} h_{j}(\tilde{x}) \\ &\leq f_{0}(\tilde{x}) \end{aligned}$$

設原本問題公式一最佳解時的 $x$ 為 $x^{\star}$ ，由於 $x^{\star}$ 必須滿足 滿足 $f_{i}(x^{\star}) \leq 0$ 和 $h_{j}(x^{\star}) = 0$ 這兩個條件，又因 $\lambda \succeq 0$ ，故 $g(\lambda, \nu) \leq p^{\star}$ 成立。

舉個例子，下圖中，黑色的實線為目標函數 $f_{0}(x)$ ，此最佳化問題有一個不等式條件限制 $f_{1}(x)$ ，用綠色虛線表示，而滿足於 $f_{1}(x) \leq 0$ 的 $x$ 範圍落在 $[-0.46~0.46]$ 之間，範圍用兩條鉛直的紅色虛線表示。 紫色的圓圈為最佳解的點 $x^{\star} = -0.46, p^{\star} = 1.54$ 。此最佳化問題沒有等式條件，故沒有 $h_{j}$ 及 $\nu_{j}$ 。則此問題的 Lagrangian 為 $L(x, \lambda)$ 。藍色的點為 $\lambda = 0.1, 0.2, ... , 1.0$ 所畫出來的 Lagrangian 圖形。

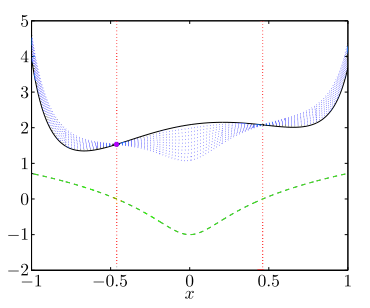
在上圖中，兩條紅色虛線之間的範圍內，即 $x$ 滿足不等式的條件限制 $f_{1}(x) \leq 0$ ，此時藍色的虛線皆位於黑色線的下方，滿足 $L(x, \lambda) \leq f_{0}(x)$ 。

下圖畫出改變不同 $\lambda$ 值時，對偶函數 $g(\lambda) = \inf_{x}( L(x, \lambda) )$ 的值，其中，黑色的實線為 $g(\lambda)$ ，紫色的虛線為 $p^{\star}$ 的值（$p^{\star} = 1.54$ ）。

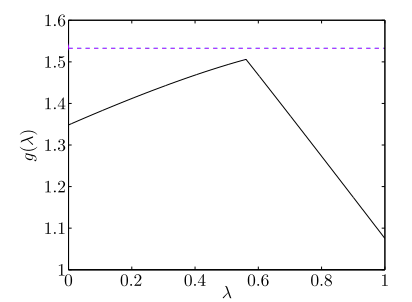
根據此圖，黑色的線恆在紫色的虛線下方，滿足 $g(\lambda) \leq p^{\star}$ 。

The Lagrange dual problem

所謂的對偶問題（Lagrange dual problem）即是把原本的問題轉成對偶函數之後，來解最佳化問題。

從前面結論可得知，對偶函數若滿足 $\lambda \succeq 0$ （也就是所有的 $\lambda_{i}$ 都滿足 $\lambda_{i} \geq 0$ ）的條件，則必足 $g(\lambda, \nu) \leq p^{\star}$ 。如果想找出最接近 $p^{\star}$ 的對偶函數解，則可藉由改變 $\lambda, \nu$ ，來找出 $g(\lambda, \nu)$ 的最大值。此對偶問題如下 ＜公式二＞：

$$\begin{aligned} & \textbf{maximize} & g(\lambda, \nu) & \\ & \textbf{subject to } & \lambda \succeq 0 \\ \end{aligned}$$

如果可以找出一組解，滿足 $\lambda \succeq 0$ ，可得出 $g(\lambda, \nu)$ 的最大值 $d^{\star}$ ，則此問題滿足 dual feasibility。

根據對偶問題的解 $d^{\star}$ 和原本問題的解 $p^{\star}$ 的關係，可將對偶性質分為 weak duality 和 strong duality 兩類：

Weak duality

若對偶問題的解，小於或等於原本問題的解，即滿足 weak duality ：

$$d^{\star} \leq p^{\star}$$

根據前面段落 Lower bounds on optimal value 所推導的結論， Weak duality 必定成立。

Strong duality

若對偶問題的解，等於原本問題的解，即滿足 strong duality ：

$$d^{\star} = p^{\star}$$

這個條件不一定會成立，如果要成立的話，原本問題公式一的中的 $f_{0}(x)$ 和 $f_{i}(x)$ 要是凸函數，但即使滿足此條件，仍須滿足其他條件才能使 strong duality 成立，這講起來比較複雜，在此先不提。

Complementary Slackness

設原本問題最佳解的 $x$ 為 $x^{\star}$ ，對偶問題最佳解的 $(\lambda, \nu)$ 為 $(\lambda^{\star}, \nu^{\star})$ ，根據對偶函數 $g(\lambda^{\star}, \nu^{\star})$ 的定義，和前面段落 Lower bounds on optimal value 所推導出的結論，可得出：

$$\begin{aligned} & g(\lambda^{\star}, \nu^{\star}) = \inf_{x}( L(x, \lambda^{\star}, \nu^{\star}) ) \\ & \leq f_{0}(x^{\star}) + \sum_{i=1}^{m} \lambda_{i}^{\star} f_{i}(x^{\star}) + \sum_{j=1}^{p} \nu_{j}^{\star} h_{j}(x^{\star}) \\ & \leq f_{0}(x^{\star}) \end{aligned}$$

若對偶問題滿足 strong duality ：

$$g(\lambda^{\star}, \nu^{\star}) = f_{0}(x^{\star})$$

則須滿足：

$$\begin{aligned} & \sum_{i=1}^{m} \lambda_{i}^{\star} f_{i}(x^{\star}) = 0 \mspace{40mu} \text{(a)} \\ & \sum_{j=1}^{p} \nu_{j}^{\star} h_{j}(x^{\star}) = 0 \mspace{40mu} \text{(b)} \end{aligned}$$

由於 $h_{j}(x^{\star}) = 0$ 為原本問題的等式條件限制，故 (b) 必會成立，若 (a) 要成立的話，須滿足：

$$\lambda_{i}^{\star} f_{i}(x^{\star}) = 0 \mspace{20mu} \textbf{for } i=1,2,...m$$

也就是說，$f_{i}(x^{\star})$ 和 $\lambda_{i}^{\star}$ 的其中一項必須為零，不可以兩項都不為零。這種情形稱為 complementary slackness ，也就是林軒田教授在機器學習技法課程中所提到的：

哈利波特和佛地魔，其中一個必須死掉。

Karush-Kuhn-Tucker (KKT) conditions

KKT conditions 即為下四個條件：

1. Primal Feasibility：即滿足原本問題公式一的限制條件 $f_{i}(x) \leq 0$ 和 $h_{j}(x) = 0$ ，使原本問題有解。

2. Dual Feasibility：即滿足對偶問題公式二的限制條件： $\lambda \succeq 0$ ，使對偶問題有解。

3. Complementary Slackness：即滿足 strong duality ：$g(\lambda^{\star}, \nu^{\star}) = f_{0}(x^{\star})$ ，使原本問題和對偶問題有相同解。

4. Stationarity（gradient of Lagrangian with respect to x vanishes）：

$$\nabla f_{0}(x^{\star}) + \sum_{i=1}^{m} \lambda_{i} \nabla f_{i}(x^{\star}) + \sum_{j=1}^{p} \nu_{j} \nabla h_{j}(x^{\star}) = 0$$

第四項雖然前面沒提到，但很容易理解，也就是說，在得出最佳解 $x^{\star}$ 的時候， Lagrangian 對於 $x^{\star}$ 的 gradient 要等於 0 。

Reference

本文參考至以下教科書，本文中的圖片也取自於以下教科書：

Stephen Boyd & Lieven Vandenberghe. Convex Optimization. Chapter 5 Duality.