Introduction
在做 Logistic Regression的時候,可以用 gradient descent 來做訓練,而類神經網路本身即是很多層的 Logistic Regression 所構成,也可以用同樣方法來做訓練。
但類神經網路在訓練過程時,需要分為兩個步驟,為: Forward Phase 與 Backward Phase 。 也就是要先從 input 把值傳到 output,再從 output 往回傳遞 error 到每一層的神經元,去更新層與層之間權重的參數。
Forward Phase
在 Forward Phase 時,先從 input 將值一層層傳遞到 output。
對於一個簡單的神經元 ,如下圖 <圖一>:
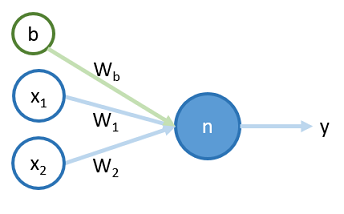
將一筆訓練資料 和 bias 輸入到神經元 到輸出的過程,分成兩步,分別為 , ,過程如下:
在輸入神經元時, 先將 input 值和其權重作乘積。
在輸出神經元時, 將 的值用 sigmoid function 轉成值範圍從 0 到 1 的函數。
傳遞到 後,可與訓練資料的答案 用 cost function 來計算其差值,並用 backward propagation 修正權重 、 和 。
對於一個簡單的類神經網路,共有兩層,四個神經元,如下圖<圖二>:
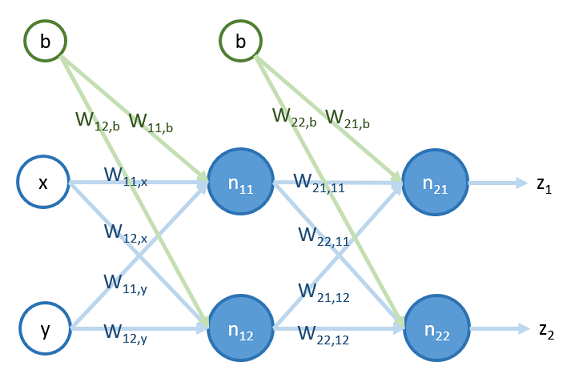
其值傳遞的過程如下:
1.把 和 和 bias 傳入到第一層神經元 及 :
其中, 表示傳入神經元 的值,而 表示傳出神經元 的值,而 表示值從 傳入 時,所乘上的權重
2.第一層神經元將其輸出值 和 傳到第二層神經元 和 :
傳遞完後,可與訓練資料的答案 和 用 cost function 來計算其差值,並用 backward propagation 修正權重。
Derivation of Gradient Descent
在講解 backward Phase 之前,先推導類神經網路的 gradient descent 公式和 backward propagation 的原理:
對於<圖一>中的一個簡單的神經元 ,將一筆訓練資料 傳遞到 所得出的值和 的值做比較,我們可用以下的 cost function 來計算:
從以上 cost function 可得知,如果 和 都等於 0 ,或者都等於 1 ,則 cost 會是 0 ,若 和 其中有一個是 1 ,而另一個是 0 ,則 cost 會趨近於無限大。
用 gradient Descent 調整 、 和 來做訓練時,可用以下公式<公式一>:
其中, 為 learning rate ,用來控制訓練的速度。
接著要推導這個公式怎麼算,首先,將 的微分用 chain rule 展開,如下 <公式二>:
以上公式,總共有 、 與 三個部份的微分要算。
1.:
2.:
3.:
代入以上三個結果到<公式二>,可得出 的值,如下:
同理可得出 與 的值,分別為:
其中, 的結果為:
將 、 和 的結果代入<公式一>,得出:
Derivation of Backward Propagation
若要推導超過一層的類神經網路的 gradient descent 公式,就要用到 backward propagation 。
對於<圖二>中的一個簡單的類神經網路,它的 cost function 如下:
對於最後一層與倒數第二層之間的權重改變,可用 gradient descent ,如下<公式三>:
可用先前推導出單一神經元時的微分結果,得出:
同理可求出 、 和 相對應的公式。
在要推導更往前一層的權重變化公式之前,先觀察以上公式,發現它們有共同的部分: ,可以用 來表示這個值,即:
的物理意義如下圖所示:
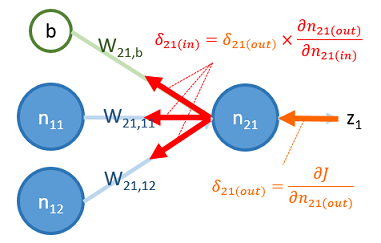
圖中, 是 在神經元 輸出點的微分值,可以把 看成是 從神經元 的輸出點往回傳到輸入點,即乘上 。因此,這過程又稱為 backward propagation 。
將 置換到<公式三>,得出這一層推導的最後結果:
同理, 的 gradient descent 公式,也可用相同方法推導出來:
再來,要推導更往前一層的權重變化公式,要用 gradient descent <公式四>:
舉 為例,用 chain rule 求出 的值,如下<公式五>:
其中, 、 、 和 這四項的值分別為:
再代入這些值與之前推導出的 和 的值到<公式五>,可求出 為:
同理,可求出 和 的值分別為:
如同前一層所推導的,以上公式也有相同部分,也可以用 來簡化它們,如下:
可把 用後面層傳回來的的 來表示,如下:
這些 的物理意義如下圖所示:
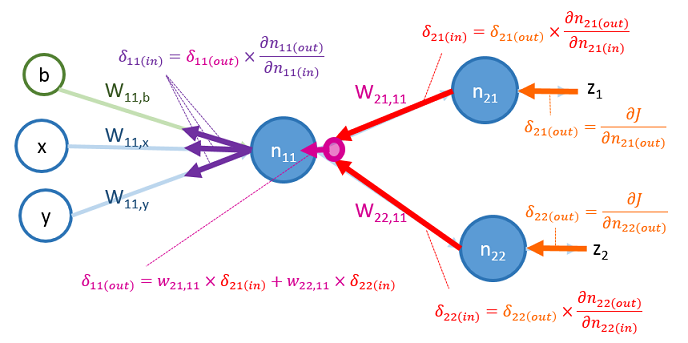
從圖中可以看到, 是 由 和 往反方向傳遞,再乘上其權重 與 所得出的 。
將 置換到<公式四>,得出這一層推導的最後結果:
同理, 的 gradient descent 的公式,也可用相同方法推導出來:
Backward Phase
backward phase 要做的即是 backward propagation ,也就是從 output 把 算出來,並更新權重 ,再把 往回傳一層,再更新那層的權重 ,這樣一直傳下去直到 input 。
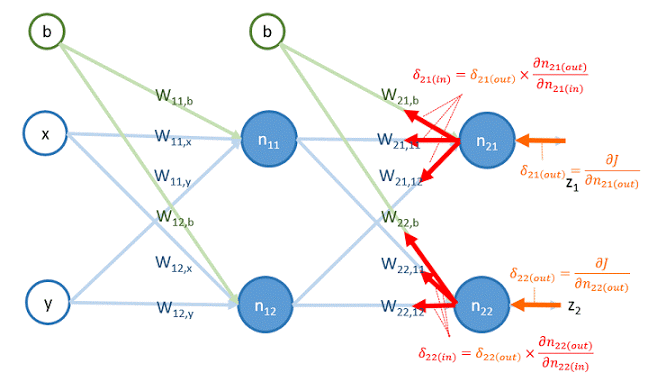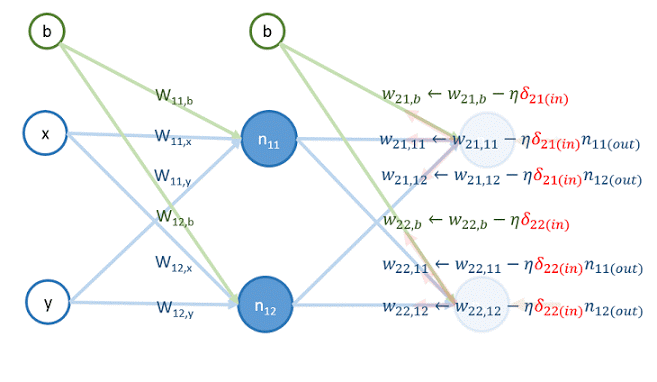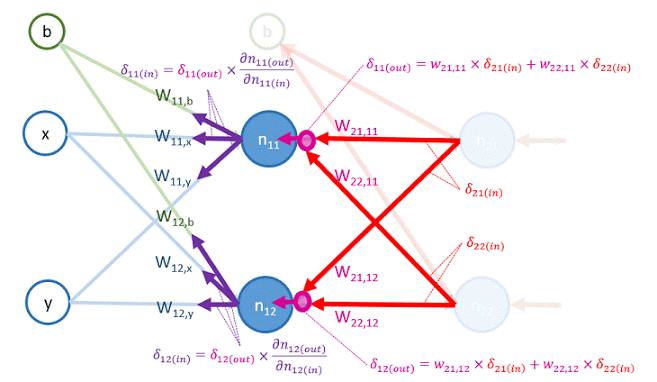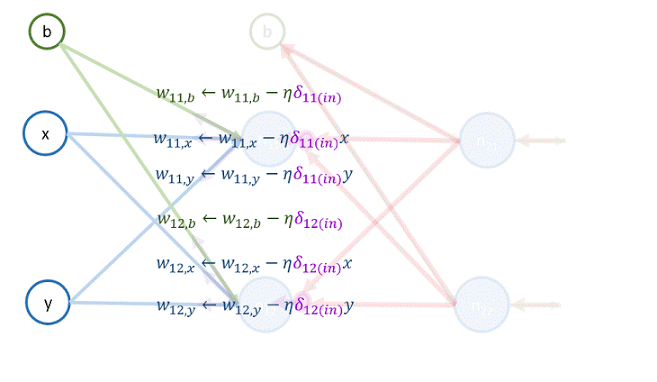
首先,把 和 算出來:
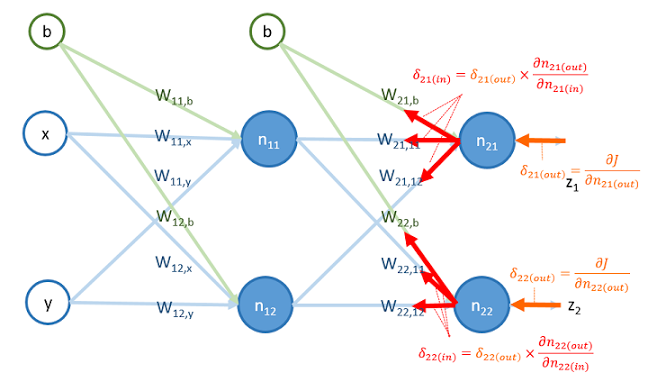
再來,用 和 更新以下權重的值:
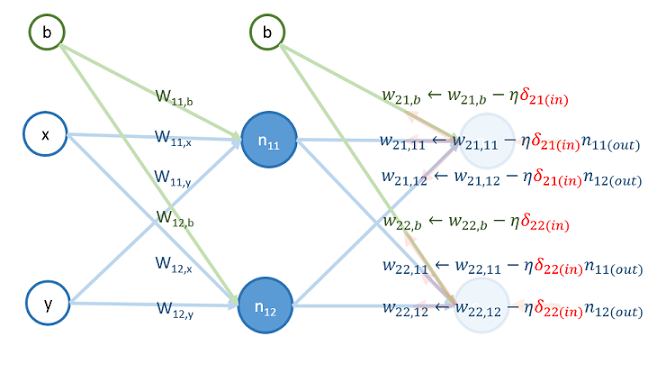
再來,把 和 乘上權重,算出 和 的值:
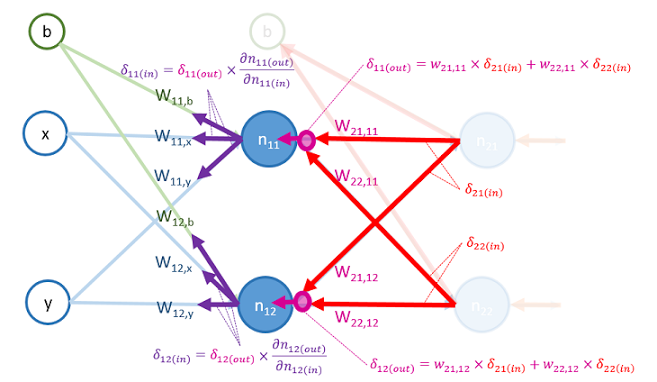
最後,用 和 更新以下權重的值:
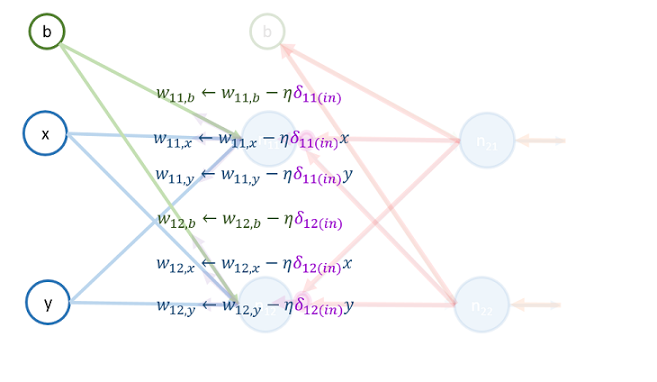
更新完後,即結束了在資料 上的這一輪訓練。
以下為整個過程的動畫版:
Reference
本文參考 coursera 課程 Andrew Ng. Machine Learning
https://www.coursera.org/course/ml