Mark Chang's Blog

Machine Learning, Deep Learning and Python

Perceptron Algorithm

1.Introduction

這次來講一下機器學習(Machine Learning)

簡而言之,Machine Learning是一種讓機器根據已知的data,預測出未知的data情形如何

現在,來看看一種簡單的Machine Learning演算法

叫作Perceotron Algorithm

Peceptron Algorithm要做的事

就是要讓電腦學習,怎樣畫一條線,把兩群不同的資料分開

2.Load Data

接著來看看要怎麼實作Perceptron Algorithm

首先,開啟新的檔案 perceptron.py 並載入模組

perceptron.py
1
2

import numpy as np
import matplotlib.pyplot as plt

給定一筆資料

perceptron.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

X1 = np.array([-0.62231486, -0.96251306,  0.42269922, -1.452746  , -0.66915783,
               -0.35716016,  0.49505163, -1.8117848 ,  0.53376487, -1.86923838,
                0.71434306, -0.4055084 ,  0.82887254,  0.81221287,  1.44280951,
               -0.45599278, -1.16715888,  1.08913131, -1.61470741,  1.61113001,
               -1.4532688 ,  1.04872588, -1.52312195, -1.62831727, -0.25191539])

X2 = np.array([-1.67427011, -1.81046748,  1.20384694, -0.41572751,  0.66851908,
               -1.75435288, -1.57532207, -1.22329618, -0.84375819,  0.52873296,
               -1.10837773,  0.04612922,  0.67696196,  0.84618152, -0.77362548,
                0.99153072,  1.7896494 , -0.38343121, -0.21337742,  0.64754817,
                0.36719101,  0.23132427,  1.07029963,  1.62919909, -1.53920827])

Y = np.array([  1.,  -1.,  -1.,  -1.,  -1.,
                1.,   1.,  -1.,   1.,  -1.,
                1.,  -1.,   1.,   1.,   1.,
               -1.,  -1.,   1.,  -1.,   1.,
               -1.,   1.,  -1.,  -1.,   1.])

其中 X1 是資料的X座標, X2 是資料的Y座標, Y是資料的分類的結果, 不是Y座標

然後寫個function 把data畫出來

perceptron.py 
1
2
3
4
5
6
7
8
9

def plot_data(filename = 'data0'):
    fig = plt.figure()
    ax = fig.add_subplot(111)
    plt.scatter(X1[Y >= 0], X2[Y >= 0], s = 80, c = 'b', marker = "o")
    plt.scatter(X1[Y <  0], X2[Y  < 0], s = 80, c = 'r', marker = "^")
    ax.set_xlim(xl1, xl2)
    ax.set_ylim(yl1, yl2)
    fig.set_size_inches(6, 6)
    plt.show()

到interactive mode執行

1
2

>>> import perceptron as pct
>>> pct.plot_data()

這個圖把藍色( ),和紅色( )兩群資料呈現出來

3.Draw Line

再來,看看怎麼畫一條線

先在 perceptron.py 檔案新增一個畫線的function

我們要畫的這條線有兩個參數,分別是

這條線的直線方程式是:

藉由改變 的數值,我們可以控制這條線的斜率

*註:

事實上若只有只可以改變線的斜率,必須再另外再加個常數相才可改變線的位置

本文提到的是較簡化的模型,故省略常數項*

perceptron.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

def plot_data_and_line(w0,w1,w2):
    w1,w2 = float(w1),float(w2)
    if w2 != 0 :
        y1,y2 = (-w1*(xl1))/w2, (-w1*(xl2))/w2
        vx1,vy1 = [xl1,xl2,xl2,xl1,xl1], [y1,y2,yl2,yl2,y1]
        vx2,vy2 = [xl1,xl2,xl2,xl1,xl1], [y1,y2,yl1,yl1,y1]
    elif w1 != 0:
        vx1,vy1 = [xl2,0,0,xl2,xl2], [yl1,yl1,yl2,yl2,yl1]
        vx2,vy2 = [xl1,0,0,xl1,xl1], [yl1,yl1,yl2,yl2,yl1]
    else:
        print "ERROR, Invalid w1 and w2."
        return;
    if  w2 > 0 or ( w2 == 0 and w1 > 0):
        c1,c2 = 'b','r'
    else:
        c1,c2 = 'r','b'
    fig = plt.figure()
    ax = fig.add_subplot(111)
    plt.scatter(X1[Y > 0], X2[Y > 0], s = 80, c = 'b', marker = "o")
    plt.scatter(X1[Y<= 0], X2[Y<= 0], s = 80, c = 'r', marker = "^")
    plt.fill(vx1, vy1, c1, alpha = 0.25)
    plt.fill(vx2, vy2, c2, alpha = 0.25)
    ax.set_title(("w1 = %s, w2 = %s")%( w1, w2))
    ax.set_xlim(xl1, xl2)
    ax.set_ylim(yl1, yl2)
    fig.set_size_inches(6, 6)
    plt.show()

程式碼有點多,但其實是為了處理某些special case,例如 ` w2 != 0 :` 是用來判斷斜率是否為無限大

到interactive mode載入模組

1
2

>>> reload(pct)
<module 'perceptron' from 'perceptron.py'>

接著你可以試著輸入不同的參數,讓電腦畫出不同的線,例如：

1
2
3
4

>>> pct.plot_data_and_line(1,1)
>>> pct.plot_data_and_line(1,2)
>>> pct.plot_data_and_line(1,0.5)
>>> pct.plot_data_and_line(-1,-1)

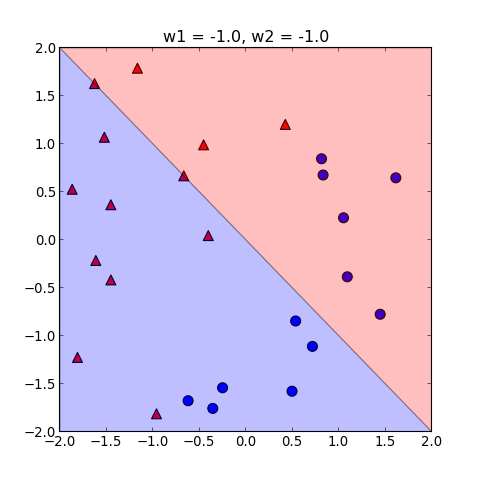
這樣就可以畫出不一樣的線了

改變數字大小,可控制斜率

改變正負號,可以把紅色或藍色的區域反轉過來

4. Perceptron Algorithm

接下來,我們要讓電腦自己去學習,該怎麼樣畫一條線把資料分開

Peceptron Algorithm 的概念是這樣

先隨便給一條線,然後再根據這條線分類錯誤做修正

我們先給定畫出一條線,如下圖

從上圖中分類錯誤的點中,任意挑一個點 ,

用 到原點的向量 ,來修正直線的法向量

要怎麼修正呢？要看 的類別 來決定, 調整 的方向

公式如下：

用這個方法就可以改變直線的斜率,把分類錯誤的點 ,歸到正確的一類,

舉例：

1.藍色( )分類錯誤

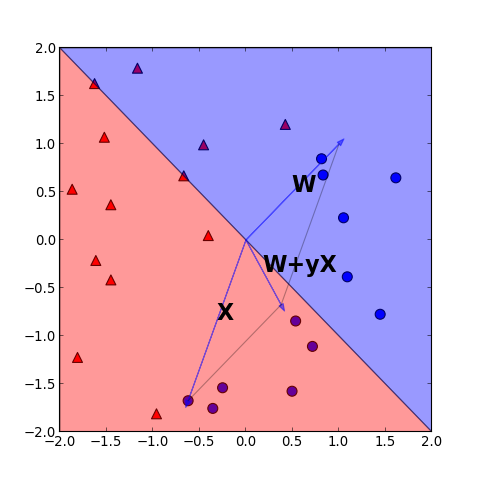
修正後如下

2.紅色( )分類錯誤

修正後如下

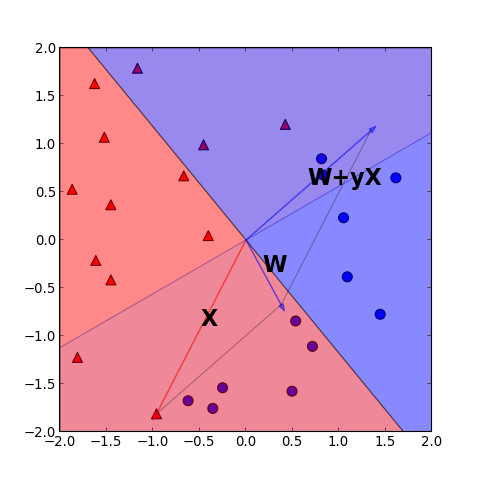
以上結果顯示, 修正過後, 有可能會把原本分類正確的點,分類到錯的一類

所以可能要重複修正好幾次,直到把所有的點都分類正確為止

所以Perceptron的演算法如下：

(1) 任選一條線

(2) 從這條線中選一個分類錯誤的點x

(3) 由點x修正線的斜率

(4) 重複(2)直到所有的點都分類正確

我們把這個演算法寫到 perceptron.py 裡

perceptron.py
1
2
3
4
5
6
7
8
9
10
11

def learn_perceptron(times=1000):
    w1,w2 = 1,1
    for i in range(times):
        ERR = (w1*X1+w2*X2) * Y < 0
        if len(filter(bool,ERR)) > 0:
           err_x1,err_x2,err_y = X1[ERR][0],X2[ERR][0],Y[ERR][0]
           w1,w2 = (w1+err_y*err_x1),(w2+err_y*err_x2)
        else:
           print "Complete!"
           break;
    plot_data_and_line(w1,w2)

寫好之後,到interactive mode載入模組後,

其中times是迴圈的最大重複次數,

如果超過這個次數後還沒有完全分類正確,則演算法停止

1
2
3
4
5
6
7
8
9
10

>>> reload(pct)
<module 'perceptron' from 'perceptron.py'>

>>> pct.learn_perceptron()
Iteration:1
Iteration:2
Iteration:3
Iteration:4
Iteration:5
Complete!

總共執行了五次迴圈,所有的分類就都正確了

執行結果如下：

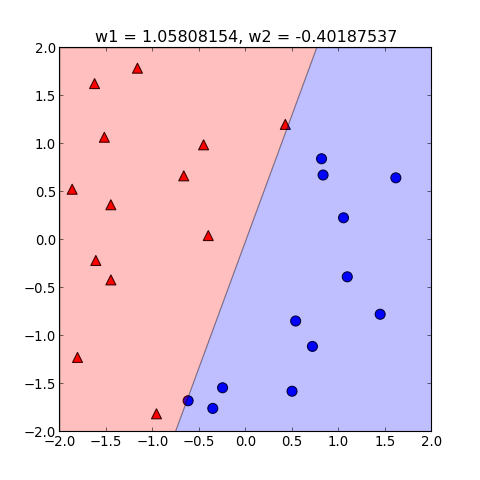
如果想要看看每一次迴圈中修正 的情形

以下提供更詳盡過程分解

但程式碼有點長

perceptron.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

def learn_and_plot():
    w1,w2 = 1.,1.
    plt.ion()
    fig = plt.figure()
    plt.show()
    complete=False
    i=0
    while True:
        plt.clf()
        ax = fig.add_subplot(111)
        ERR = (w1*X1+w2*X2) * Y < 0
        if i > 0 and (not complete):
            pwa1,pwa2 = pw1+err_y*err_x1,pw2+err_y*err_x2
            if err_y >=0:
                eva1,eva2=[err_x1,pwa1], [err_x2,pwa2]
                ac='b'
            else:
                eva1,eva2=[err_x1,pw1], [err_x2,pw2]
                ac='r'
            evb1,evb2=[pwa1,pw1], [pwa2,pw2]
            ax.arrow(0, 0, err_x1, err_x2, head_width=0.05, alpha=0.5, fc=ac, ec=ac )
            ax.arrow(0, 0, pw1, pw2, head_width=0.05, alpha=0.5, fc='b', ec='b')
            ax.arrow(0, 0, pwa1, pwa2, head_width=0.05, alpha=0.5, fc='b', ec='b')
            plt.text(err_x1/2., err_x2/2., 'X', color='k', size=20, fontweight='bold')
            plt.text(pw1/2., pw2/2., 'W', color='k', size=20, fontweight='bold')
            plt.text(pwa1/2., pwa2/2.,'W+yX', color='k', size=20, fontweight='bold')
            plt.plot(eva1, eva2, alpha=0.3, color='k')
            plt.plot(evb1, evb2, alpha=0.3, color='k')
            plt.plot([xl1,xl2],[y1,y2],alpha=0.2, color='b')
            plt.fill(pvx1, pvy1, c1, alpha = 0.1)
            plt.fill(pvx2, pvy2, c2, alpha = 0.1)
        if w2 != 0 :
            y1,y2 = (-w1*(xl1))/w2, (-w1*(xl2))/w2
            vx1,vy1 = [xl1,xl2,xl2,xl1,xl1], [y1,y2,yl2,yl2,y1]
            vx2,vy2 = [xl1,xl2,xl2,xl1,xl1], [y1,y2,yl1,yl1,y1]
        elif w1 != 0:
            vx1,vy1 = [xl2,0,0,xl2,xl2], [yl1,yl1,yl2,yl2,yl1]
            vx2,vy2 = [xl1,0,0,xl1,xl1], [yl1,yl1,yl2,yl2,yl1]
        else:
            print "ERROR, Invalid w1 and w2."
            return;
        if  w2 > 0 or (w2 == 0 and w1 > 0):
            c1,c2 = 'b','r'
        else:
            c1,c2 = 'r','b'
        plt.scatter(X1[Y > 0], X2[Y > 0], s = 80, c = 'b', marker = "o")
        plt.scatter(X1[Y<= 0], X2[Y<= 0], s = 80, c = 'r', marker = "^")
        ax.set_title( ("Iteration:%s, w1 = %.5f, w2 = %.5f")%(i, w1, w2) )
        ax.set_xlim(xl1, xl2)
        ax.set_ylim(yl1, yl2)
        if not complete:
            plt.show()
            fig.set_size_inches(6, 6)
            raw_input("Please press ENTER to update the result of iteration.")
        plt.fill(vx1, vy1, c1, alpha = 0.4)
        plt.fill(vx2, vy2, c2, alpha = 0.4)
        pw1,pw2,pvx1,pvy1,pvx2,pvy2 = w1,w2,vx1,vy1,vx2,vy2
        #----Perceptron Algorithm-------# 
        ERR = (w1*X1+w2*X2) * Y < 0
        if len(filter(bool,ERR)) > 0:
           err_x1,err_x2,err_y = X1[ERR][0],X2[ERR][0],Y[ERR][0]
           w1,w2 = (w1+err_y*err_x1),(w2+err_y*err_x2)
        else:
           if complete:
               ax.set_title(("Complete! Iteration:%s, w1 = %.5f, w2 = %.5f")%(i-1, w1, w2))
               plt.show()
               fig.set_size_inches(6, 6)
               print "Complete!"
               break
           else:
              complete=True
        #-----------------------#
        plt.show()
        fig.set_size_inches(6, 6)
        i=i+1
        raw_input("Please press ENTER to start the next iteration.")

然後,到interactive mode跑看看這個function

1
2
3
4
5
6
7

>>> reload(pct)
<module 'perceptron' from 'perceptron.py'>

>>> pct.learn_and_plot()
Please press ENTER to update the result of iteration.
Please press ENTER to start the next iteration.
....

進行完每次計算時,程式會把圖畫出來

然後程式會暫停,要按下ENTER才能繼續進行下一步

執行結果如下：

5. Further Reading

以上是Perceptron Algorithm很簡單的介紹

但其實Perceptron Algorithm有其他變化形式

例如,如果有noise存在的時候,本篇介紹的演算法就無法求得最佳解

就要用其他的變化形式來處理

想要看更多相關介紹,請到coursera上線上課程

1.Andrew Ng. Machine Learning

https://www.coursera.org/course/ml

2.林軒田 機器學習基石 (Machine Learning Foundations)

https://www.coursera.org/course/ntumlone

Comments